2.4 Linear Functions

Let’s say you hop into a taxi in Las Vegas, the meter immediately reads $3.30; this is the “drop” charge made when the taximeter is activated.  After that initial fee, the taximeter will add $2.60 for each mile the taxi drives[1].  In this scenario, the total taxi fare depends upon the number of miles ridden in the taxi, and we can ask whether it is possible to model this type of scenario with a function. Using descriptive variables, we choose m for miles and C for Cost in dollars as a function of miles: C(m).

We know for certain that C(0)=3.30 since that is the drop charge assessed regardless of how many miles are driven. Since 2.60 is added for each mile driven, then C(1)=3.30+2.60=5.90.

If we drove a second mile, another 2.60 would be added to the cost: C(2)=3.30+2.60+2.60=3.30+2.60(2)=8.50.

If we drove a third mile, another 2.60 would be added to the cost: C(2)=3.30+2.60+2.60 +2.60=3.30+2.60(3)=11.10.

From this we observe the pattern, and conclude that if m miles are driven, C(m)=3.30+2.60m because we start with a $3.30 drop fee and then for each mile increase we add $2.60.

It is good to verify that the units make sense in this equation.  The 3.30 drop charge is measured in dollars; the 2.60 charge is measured in dollars per mile.  So: C(m)=3.30\;dollars+\left(2.60\dfrac{dollars}{miles}\right)(m\;miles)

When dollars per mile are multiplied by a number of miles, the result is a number of dollars, matching the units on the 3.30, and matching the desired units for the C function.

Notice this equation C(m)=3.30+2.60m consisted of two quantities.  The first is the fixed $3.30 charge which does not change based on the value of the input.  The second is the $2.60 dollars per mile value, which is a rate of change.  In the equation this rate of change is multiplied by the input value.

Looking at this same problem in table format we can also see the cost changes by 2.60 for every 1 mile increase.

m 0 1 2 3
C(m) 3.30 5.90 8.50 11.10

It is important here to note that in this equation, the rate of change is constant; over any interval, the rate of change is the same.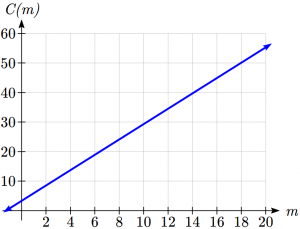Graph of the equation C(m)=3.30+2.60m

Graphing this equation, C(m)=3.30+2.60m we see the shape is a line, which is how these function get their name: linear functions.

When the number of miles is zero the cost is $3.30, giving the point (0, 3.30) on the graph.  This is the vertical intercept.  The graph is increasing in a straight line from left to right because for each mile the cost goes up by $2.60; this rate remains consistent.

In this example you have seen the taxi cost modeled in words, an equation, a table and in graphical form.  Whenever possible, ensure that you can link these four representations together to continually build your skills.  It is important to note that you will not always be able to find all 4 representations for a problem and so being able to work with all 4 forms is very important.

Linear Function

A linear function is a function whose graph produces a line. Linear functions can always be written in the form

    \[ f(x)=b+mx \quad \textsf or \quad f(x)=mx+b \]

where b is the initial or starting value of the function (when input, x=0) and m is the constant rate of change of the function

Take NoteYou may be more used to f(x)=mx+b or y=mx+b from other math classes, but thinking about linear functions as f(x)=b+mx tends to help more with thinking about these in applications because it corresponds to the way we speak: “The output starts at b and increases at a rate of m.”  For this reason, we will use f(x)=b+mx form for many of the example, but just remember, they are equivalent and can be written correctly both ways.

Slope and Increasing/Decreasing

m is the constant rate of change of the function (also called slope).  The slope determines if the function is an increasing function or a decreasing function.

f(x)=b+mx is an increasing function if m>0.
f(x)=b+mx is a decreasing function if m<0.

If m=0 the rate of change is zero, and the function f(x)=b+0x=b which is just f(x)=b and is a horizontal line passing through the point(0,b), neither increasing nor decreasing.

Example: Writing a Linear Function

To start producing a new model of custom wheels, a company will have to purchase $30,000 in new equipment.  Each wheel made costs them $40 in supplies and labor.  Write a formula for the total cost, TC, of producing q wheels.  What will be their total costs in the first year if they expect to sell 240 wheels?

The initial value,b, for this function is 30,000, since that is the startup costs, so TC(0)=30,000. The cost increases by 40 for each wheel made, so the rate of change, m, is 40 dollars per wheel. With this information, we can write the formula:
TC(q)=30,000+40q.

Since m>0, TC(q) is an increasing linear function.

With this formula, we can predict the total cost of 240 wheels:
TC(24)=30,000+40(240)=30,000+9,600=39,600.

The total cost will be $39,600.

Try it Now 1

 If you earn $30,000 per year and you spend $29,000 per year write an equation for the amount of money you save after y years, if you start with nothing.

“The most important thing, spend less than you earn!” [2]

Calculating Rate of Change

Given two values for the input, x_1 and x_2, and two corresponding values for the output, y_1 and y_2, or a set of points (x_1,y_1) and (x_2, y_2), if we wish to find a linear function that contains both points we can calculate the rate of change, m:

m=\dfrac{\textsf{change in output}}{\textsf{change in input}}=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}

 

Rate of change of a linear function is also called the slope of the line.

Take NoteNote in function notation y_1=f(x_1) and y_2=f(x_2), so we could equivalently write m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}

 

Examples Calculating Rate of Change/Slope

a. The population of a city increased from 23,400 to 27,800 between 2002 and 2006.  Find the rate of change of the population during this time span.

The rate of change will relate the change in population to the change in time.  The population increased by people over the 4 year time interval.  To find the rate of change, the number of people per year the population changed by:

\dfrac{4400\;people}{4\;years}=1100\dfrac{people}{year}=1000 \textsf{people per year}

 

Notice that we knew the population was increasing, so we would expect our value for m to be positive.  This is a quick way to check to see if your value is reasonable.

b. The pressure, P, in pounds per square inch (PSI) on a diver depends upon their depth below the water surface, d in feet, following the equation P(d) = 14.696 + 0.434d.  Interpret the components of this function.

The rate of change, or slope, 0.434 would have units \dfrac{output}{input}=\dfrac{pressure}{depth}=\dfrac{PSI}{ft}. This tells us the pressure on the diver increases by 0.434 PSI for each foot their depth increases.

The initial value, 14.696 will have the same units as the output, so this tells us that at a depth of 0 feet, the pressure on the diver will be 14.696 PSI.

c. If f(x) is a linear function, f(3)=-2 and f(8)=1, find the rate of change. 

f(3)=-2 tells us that the input 3 corresponds with the output -2 and f(8)=1 tells us that the input 8 corresponds with the output 1.  So we have two points with coordinates (3,-2) and (8,1). Lets call (3,-2) our {x_1,y_1} and (8,1) our {x_2, y_2} and use the formula:

m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{1-(-2)}{8-3}=\dfrac{3}{5}  Alternatively, we could also write it as m=0.6

Warning SignIt is not necessarily important which pair of values comes first in the subtraction so long as the first output value used corresponds with the first input value used.

 

 

Try it Now 2

Given the two points (2, 3) and (0, 4), find the rate of change.  Is this function increasing or decreasing?

Writing Equations of Lines

We can now find the rate of change given two input-output pairs, and can write an equation for a linear function once we have the rate of change and initial value.  If we have two input-output pairs and they do not include the initial value of the function, then we will have to solve for it.

There are two methods for doing this.

Method 1: Use 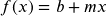f(x)=b+mx and solve for b.

In this case, we use our two points to find m and then choose one point, say (x_1,y_1) to enter in the formula, y=b+mx

You end up with y_1=b+mx_1 and subtracting mx_1 from both sides, we get b=y_1-mx_1.  This could be done with x_2 if it is easier as well.

Method 2 Point-Slope Form

For this method, we use point-slope form of a line, which is just the slope formula rearranged but with only one known point:

m=\dfrac{y-y_1}{x-x_1}

multiply (x-x_1) to both sides:  y-y_1=m(x-x_1).

Add y_1 to both sides: y=m(x-x_1)-y_1 and simplify. You then have your equation.

Examples Writing Equations of Lines

a. Write an equation for the linear function graphed to the right.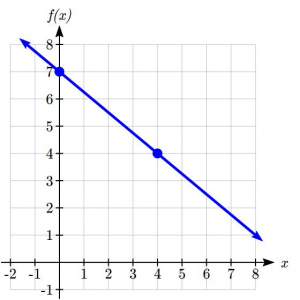Example graph of a line with a point at (0,7) and (4,4).

Looking at the graph, we might notice that is passes through the points (0,7) and (4,4). From the first value, we know the initial value of the function is b=7, so in this case we will only need to calculate the rate of change:

m=\dfrac{4-7}{4-0}=\dfrac{-3}{4}

This allows us to write the equation:

f(x)=7-\dfrac{3}{4}x

b. If f(x) is a linear function, f(3)=-2, and f(8)=1, find an equation for the function.

In a previous example, we computed the rate of change to be m=\dfrac{3}{5}. In this case, we do not know the initial value f(0) so we have to solve for it. Using method 1, we can plug in one of our points and the slope.

f(x)=b+\dfrac{3}{5}x
We know f(3) = -2 so: -2=b+\dfrac{3}{5}(3)
Simplify and solve for b:  b=-2-\dfrac{9}{5}=\dfrac{-19}{5}
Now write the equation with the m and b you have found:
f(x)=\dfrac{-19}{5}+\dfrac{3}{5}x

c. Working as an insurance salesperson, Ilya earns a base salary and a commission on each new policy, so Ilya’s weekly income, I, depends on the number of new policies, n, he sells during the week.  Last week he sold 3 new policies, and earned $760 for the week.  The week before, he sold 5 new policies, and earned $920.  Find an equation for I(n), and interpret the meaning of the components of the equation. 

The given information gives us two input-output pairs: (3,760) and (5,920). We start by finding the rate of change.

m=\dfrac{920-760}{5-3}=\dfrac{160}{2}=80

Keeping track of units can help us interpret this quantity. Income increased by $160 when the number of policies increased by 2, so the rate of change is $80 per policy. Ilya earns a commission of $80 for each policy sold during the week.

We can then solve for the initial value

I(n)=b+80n
I(3)=760 so 760=b+80(3)
Solve for b, b=760-240=520

This value is the starting value for the function. This is Ilya’s income when n=0, which means no new policies are sold. We can interpret this as Ilya’s base salary for the week, which does not depend on the number of policies sold.

Writing the final equation:

I(n)=520+80n

Our final interpretation is: Ilya’s base salary is $520 per week and he earns an additional $80 commission for each policy sold each week.

Flashback Try It Now

Looking at the previous example part c: What is a reasonable domain and range in context of the problem?

Try it Now 3

a. The balance in your college payment account, C, is a function of the number of semesters, x you attend. Interpret the function C(x)=20000-4000x in words. How many semesters of college can you pay for until this account is empty?

b. Given that f(1)=3 and f(5)=-5, write the function, f(x). Is this function increasing or decreasing?

Examples

Given the table below write a linear equation that represents the table values:

w, number of weeks 0 2 4 6
P(w), number of rats 1000 1080 1160 1240

We can see from the table that the initial value of rats is 1000 so in the linear format P(w)=b+mw,\;b=1000.

Rather than solving for m, we notice from the table that the population goes up by 80 for every 2 weeks that pass.  This rate is consistent from week 0 to week 2, 4 and 6. The rate of change is 80 rates per 2 weeks. This can be simplified to 40 rats per week and we can write:

P(w)=b+mw as P(w)=1000+40w

If you didn’t notice from the table, you could solve for the slope using any two points from the table. For example, using (2, 1080) and (6,1240),

m=\dfrac{1240-1080}{6-2}=\dfrac{160}{4}=40 rats per week.

Try it Now Answers

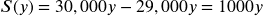  1. S(y)=30,000y-29,000y=1000y 1000 dollars saved each year.
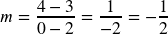  2. m=\dfrac{4-3}{0-2}=\dfrac{1}{-2}=-\dfrac{1}{2} Decreasing because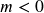 m<0
  3. a. Your college account starts with 20,000 bucks in it and you withdraw $4000 each semester, which means your account contains $20,000 and decreases by $4000 per semester.  You can pay for 5 semesters before the money in this account is gone.

b. f(x)=-2x+5

Flashback Try In Now Answer

A reasonable domain is (0,15) but answers could vary. 15 is based on selling 3 per day for a 5 day work week, but 20 or 25 could be chosen as well. Whatever is deemed as possible.

A reasonable range is (540, 1,740), The 1740 is based on the 15 from the domain, but of course if you chose a different upper bound on the domain then this range would change accordingly.

Media Attributions

  1. There is also a waiting fee assessed when the taxi is waiting at red lights, but we’ll ignore that in this discussion. ↵
  2. http://www.thesimpledollar.com/2009/06/19/rule-1-spend-less-than-you-earn/ ↵

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

College Algebra for the Managerial Sciences Copyright © by Terri Manthey is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book