2.1 Functions and Function Notation

Terri Manthey

2.1 Functions and Function Notation

What is a Function?

The natural world is full of relationships between quantities that change. When we see these relationships, it is natural for us to ask “If I know one quantity, can I then determine the other?” This establishes the idea of an input quantity, or independent variable, and a corresponding output quantity, or dependent variable. From this we get the notion of a functional relationship in which the output can be determined from the input.

For some quantities, like height and age, there are certainly relationships between these quantities. Given a specific person and any age, it is easy enough to determine their height, but if we tried to reverse that relationship and determine age from a given height, that would be problematic, since most people maintain the same height for many years.

Function

Function: A rule for a relationship between an input, or independent, quantity and an output, or dependent, quantity in which each input value uniquely determines one output value. We say “the output is a function of the input.”

Examples of Functions

a. In the height and age example above, is height a function of age? Is age a function of height?

In the height and age example above, it would be correct to say that height is a function of age, since each age uniquely determines a height. For example, on my 18th birthday, I had exactly one height of 69 inches.

However, age is not a function of height, since one height input might correspond with more than one output age. For example, for an input height of 70 inches, there is more than one output of age since I was 70 inches at the age of 20 and 21.

b. At a coffee shop, the menu consists of items and their prices. Is price a function of the item? Is the item a function of the price?

We could say that price is a function of the item, since each input of an item has one output of a price corresponding to it. We could not say that item is a function of price, since two items might have the same price.

c. In many classes the overall percentage you earn in the course corresponds to a decimal grade point. Is decimal grade a function of percentage? Is percentage a function of decimal grade?

For any percentage earned, there would be a decimal grade associated, so we could say that the decimal grade is a function of percentage. That is, if you input the percentage, your output would be a decimal grade. Percentage may or may not be a function of decimal grade, depending upon the teacher’s grading scheme. With some grading systems, there are a range of percentages that correspond to the same decimal grade.

Try it Now

Let’s consider bank account information.

1. Is your balance a function of your bank account number?
(if you input a bank account number does it make sense that the output is your balance?)

2. Is your bank account number a function of your balance?
(if you input a balance does it make sense that the output is your bank account number?)

Function Notation

To simplify writing out expressions and equations involving functions, a simplified notation is often used. We also use descriptive variables to help us remember the meaning of the quantities in the problem.

Rather than write “height is a function of age”, we could use the descriptive variable h to represent height and we could use the descriptive variable a to represent age.

Translating the words, “height is a function of age” can be accomplished if we name the function f, we write “h is f of a” or more simply h = f(a). We could instead name the function h and write h(a) which is read “h of a”

Remember we can use any variable to name the function; the notation h(a) shows us that h depends on a. The value “a” must be put into the function “h” to get a result. Be careful – the parentheses indicate that age is input into the function.

Note: do not confuse these parentheses with multiplication!

Function Notation

The notation output = f(input) defines a function named f. This would be read “output is f of input”

Examples of Function Notation

a. Introduce function notation to represent a function that takes as input the name of a month, and gives as output the number of days in that month.

The number of days in a month is a function of the name of the month, so if we name the function f, we could write “days = f(month)” or d = f(m). If we simply name the function d, we could write d(m)

For example, d(March) = 31, since March has 31 days. The notation d(m) reminds us that the number of days, d (the output) is dependent on the name of the month, m (the input)

b. A function N = f(y) gives the number of police officers, N, in a town in year y. What does f(2005) = 300 tell us?

When we read f(2005) = 300, we see the input quantity is 2005, which is a value for the input quantity of the function, the year (y). The output value is 300, the number of police officers (N), a value for the output quantity. Remember N=f(y). So this tells us that in the year 2005 there were 300 police officers in the town.

Tables as Functions

Functions can be represented in many ways: Words (as we did in the last few examples), tables of values, graphs, or formulas. Represented as a table, we are presented with a list of input and output values.

In some cases, these values represent everything we know about the relationship, while in other cases the table is simply providing us a few select values from a more complete relationship.

Table 1: This table represents the input, number of the month (January = 1, February = 2, and so on) while the output is the number of days in that month. This represents everything we know about the months & days for a given year (that is not a leap year)

(input) Month number, m	1	2	3	4	5	6	7	8	9	10	11	12
(output) Days in month, D	31	28	31	30	31	30	31	31	30	31	30	31

Table 2: The table below defines a function Q = g(n). Remember this notation tells us g is the name of the function that takes the input n and gives the output Q.

n	1	2	3	4	5
Q	8	6	7	6	8

Table 3: This table represents the age of children in years and their corresponding heights. This represents just some of the data available for height and ages of children.

(input) a, age in years	5	5	6	7	8	9	10
(output) h, height inches	40	42	44	47	50	52	54

Example of Functions as Tables

Which of these tables define a function (if any)?

Input	Output
2	1
5	3
8	6

Input	Output
-3	5
0	1
4	5

Input	Output
1	0
5	2
5	4

The first and second tables define functions. In both, each input corresponds to exactly one output. The third table does not define a function since the input value of 5 corresponds with two different output values.

Try It Now

3. If each percentage earned translated to one letter grade, would this be a function?

Solving and Evaluating Functions

When we work with functions, there are two typical things we do: evaluate and solve. Evaluating a function is what we do when we know an input, and use the function to determine the corresponding output. Evaluating will always produce one result, since each input of a function corresponds to exactly one output.

Solving equations involving a function is what we do when we know an output, and use the function to determine the inputs that would produce that output. Solving a function could produce more than one solution, since different inputs can produce the same output.

Examples Solving and Evaluating Functions

Using the table shown, where $Q=g(n)$

$n$	1	2	3	4	5
$Q$	8	6	7	6	8

a. Evaluate $g(3)$

Evaluating $g(3)$ (read: “g of 3”) means that we need to determine the output value, $Q$ , of the function $g$ given the input value of $n=3$ . Looking at the table, we see the output corresponding to $n=3$ is $Q=7$ , allowing us to conclude $g(3) = 7$ .

b. Solve $g(n) = 6$

Solving $g(n) = 6$ means we need to determine what input values, $n$ , produce an output value of $6$ . Looking at the table we see there are two solutions: $n = 2$ and $n = 4$ .

When we input $2$ into the function $g$ , our output is $Q = 6$ .

When we input $4$ into the function $g$ , our output is also $Q = 6$ .

Try it Now

4. Using the function in the example above, evaluate $g(4)$ .

Graphs as Functions

Oftentimes a graph of a relationship can be used to define a function. By convention, graphs are typically created with the input quantity along the horizontal axis and the output quantity along the vertical.

The most common graph has $y$ on the vertical axis and $x$ on the horizontal axis, and we say $y$ is a function of $x$ , or $y = f(x)$ when the function is named $f$ .

Examples of Graphs as Possible Functions

Which of these graphs defines a function $y=f(x)$ ?

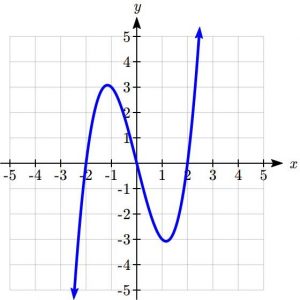
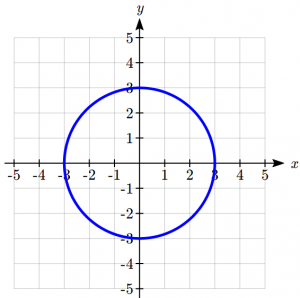
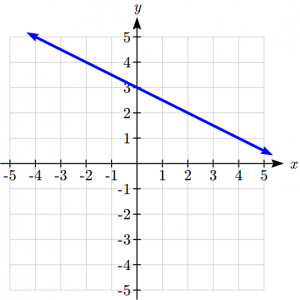
Looking at the three graphs above, the first two define a function $y=f(x)$ , since for each input value along the horizontal axis there is exactly one output value corresponding, determined by the y-value of the graph. The 3rd graph does not define a function $y=f(x)$ since some input values, such as $x=2$ , correspond with more than one output value.

Vertical Line Test

The vertical line test is a handy way to think about whether a graph defines the vertical output as a function of the horizontal input. Imagine drawing vertical lines through the graph. If any vertical line would cross the graph more than once, then the graph does not define only one vertical output for each horizontal input.

Evaluating a function using a graph requires taking the given input and using the graph to look up the corresponding output. Solving a function equation using a graph requires taking the given output and looking on the graph to determine the corresponding input.

Example to Evaluate and Solve Functions using a Graph

Given the graph shown,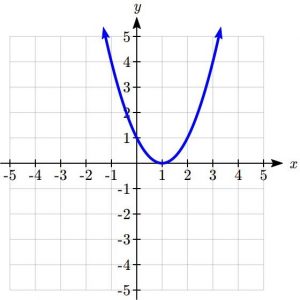

a. Evaluate $f(2)$

To evaluate $f(2)$ , we find the input of $x=2$ on the horizontal axis. Moving up to the graph gives the point $(2, 1)$ , giving an output of $y=1$ . So $f(2) = 1$ .

b. Solve $f(x) = 4$

To solve $f(x) = 4$ , we find the value 4 on the vertical axis because if $f(x) = 4$ then 4 is the output. Moving horizontally across the graph gives two points with the output of 4: $(-1,4)$ and $(3,4)$ . These give the two solutions to $f(x) = 4: x = -1$ or $x = 3$

This means $f(-1)=4$ and $f(3)=4$ , or when the input is -1 or 3, the output is 4.

Try it Now

5. Using the graph from the example above, solve $f(x)=1$ .

Formulas as Functions

When possible, it is very convenient to define relationships using formulas. If it is possible to express the output as a formula involving the input quantity, then we can define a function.

Example of Expressing a Relationship as a Functions

Express the relationship $2n+6p=12$ as a function $p=f(n)$ if possible.

To express the relationship in this form, we need to be able to write the relationship where $p$ is a function of $n$ , which means writing it as $p = (something involving n)$ .

$2n+6p=12$ subtract $2n$ from both sides

$6p=12-2n$ divide both sides by 6 and simplify

$p=\dfrac{12-2n}{6}=\dfrac{12}{6}-\dfrac{2n}{6}=2-\dfrac{1}{3}n$

Having rewritten the formula $p =$ , we can now express $p$ as a function:

$p=f(n)=2-\dfrac{1}{3}n$

It is important to note that not every relationship can be expressed as a function with a formula.

Note the important feature of an equation written as a function is that the output value can be determined directly from the input by doing evaluations – no further solving is required. This allows the relationship to act as a magic box that takes an input, processes it, and returns an output. Modern technology and computers rely on these functional relationships, since the evaluation of the function can be programmed into machines, whereas solving things is much more challenging.

As with tables and graphs, it is common to evaluate and solve functions involving formulas. Evaluating will require replacing the input variable in the formula with the value provided and calculating. Solving will require replacing the output variable in the formula with the value provided, and solving for the input(s) that would produce that output.

More Examples

1.Given the function $k(t)=t^3+2$
a. Evaluate $k(2)$
b. Solve $k(t)=1$

To evaluate $k(2)$ , we plug in the input value 2 into the formula wherever we see the input variable $t$ , then simplify.

$k(2)=2^3+2=8+2=10$

To solve $k(t)=1$ , we set the formula for $k(t)$ equal to 1, and solve for the input value that will produce that output.

$k(t) =1$
$t^3+2=1$ substitute the original formula
$t^3=-1$ subtract 2 from each side
$t=-1$ take the cube root of each side

When solving an equation using formulas, you can check your answer by using your solution in the original equation to see if your calculated answer is correct.

We want to know if is true when $k(t)=1$ when $t=-1$ , we find $k(-1).$

$k(-1)=(-1)^3+2=-1+2=1$ which was the desired result.

2. Given the function $h(p)=p^2+2p$
a. Evaluate $h(4)$
b. Solve $h(p)=3$

To evaluate $h(4)$ we substitute the value 4 for the input variable $p$ in the given function.

$h(4)=(4)^2+2(4)$

$\quad=16+8$

$\quad=24$

For part b, we need to set the function to 3 and solve:

$p^2+2p=3$ Substitute the original function

This is quadratic, so we can rearrange the equation to get it = 0

$p^2+2p-3=0$ Subtract 3 from each side

$(p+3)(p-1)=0$ Factor the quadratic

$p=-3$ or $p=1$

By the zero factor theorem since , either or (or both of them equal 0) and so we solve both equations for $p$ , finding $p = -3$ from the first equation and $p = 1$ from the second equation.