8.1 Simple and Compound Interest
Discussing interest starts with the principal, or amount your account starts with. This could be a starting investment, or the starting amount of a loan. Interest, in its most simple form, is calculated as a percent of the principal. For example, if you borrowed $100 from a friend and agree to repay it with 5% interest, then the amount of interest you would pay would just be 5% of 100: $100(0.05) = $5. The total amount you would repay would be $105, the original principal plus the interest.
Simple One-time Interest
![]()
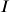 is the interest
is the interest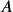 is the end amount: principal plus interest
is the end amount: principal plus interest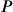 is the principal (starting amount)
is the principal (starting amount) is the interest rate in decimal form. Example: 5% = 0.05
is the interest rate in decimal form. Example: 5% = 0.05
Example of Simple Interest
A friend asks to borrow $300 and agrees to repay it in 30 days with 3% interest. How much interest will you earn?
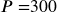 The principal
The principal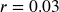 3% rate
3% rate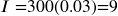 You will earn $9 interest.
You will earn $9 interest.
One-time simple interest is only common for extremely short-term loans. For longer term loans, it is common for interest to be paid on a daily, monthly, quarterly, or annual basis. In that case, interest would be earned regularly. For example, bonds are essentially a loan made to the bond issuer (a company or government) by you, the bond holder. In return for the loan, the issuer agrees to pay interest, often annually. Bonds have a maturity date, at which time the issuer pays back the original bond value.
Example of Annual Simple Interest
Suppose your city is building a new park, and issues bonds to raise the money to build it. You obtain a $1,000 bond that pays 5% interest annually that matures in 5 years. How much interest will you earn?
Each year, you would earn 5% interest: $1000(0.05) = $50 in interest. So over the course of five years, you would earn a total of $250 in interest. When the bond matures, you would receive back the $1,000 you originally paid, leaving you with a total of $1,250.
We can generalize this idea of simple interest over time.
Simple Interest over Time
![]()
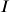 is the interest
is the interest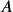 is the end amount: principal plus interest
is the end amount: principal plus interest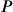 is the principal (starting amount)
is the principal (starting amount) is the interest rate in decimal form.
is the interest rate in decimal form.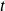 is time
is time
The units of measurement (years, months, etc.) for the time should match the time period for the interest rate.
APR – Annual Percentage Rate
Interest rates are usually given as an annual percentage rate (APR) – the total interest that will be paid in the year. If the interest is paid in smaller time increments, the APR will be divided up.
For example, a 6% APR paid monthly would be divided into twelve 0.5% payments.
A 4% annual rate paid quarterly would be divided into four 1% payments.
Example: Simple Interest over Time
Treasury Notes (T-notes) are bonds issued by the federal government to cover its expenses. Suppose you obtain a $1,000 T-note with a 4% annual rate, paid semi-annually, with a maturity in 4 years. How much interest will you earn?
Since interest is being paid semi-annually (twice a year), the 4% interest will be divided into two 2% payments.
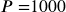 The principal
The principal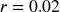 2% rate per half-year
2% rate per half-year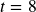 4 years = 8 half-years
4 years = 8 half-years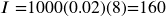 You will earn $160 interest total over the four years.
You will earn $160 interest total over the four years.
Try it Now 1
A loan company charges $30 interest for a one month loan of $500. Find the annual interest rate they are charging.
Compound Interest
With simple interest, we were assuming that we pocketed the interest when we received it. In a standard bank account, any interest we earn is automatically added to our balance, and we earn interest on that interest in future years. This reinvestment of interest is called compounding. We looked at this situation earlier, in the chapter on exponential growth.
Compound Interest
![]()
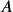 is the balance in the account after t years
is the balance in the account after t years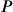 is the starting balance of the account (also called initial deposit, or principal)
is the starting balance of the account (also called initial deposit, or principal) is the annual interest rate in decimal form.
is the annual interest rate in decimal form.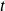 is the number of years
is the number of years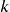 is the number of compounding periods in one year.
is the number of compounding periods in one year.
- If the compounding is done annually (once a year),
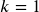 .
. - If the compounding is done quarterly (every 3 months),
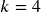 .
. - If the compounding is done monthly,
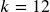 .
. - If the compounding is done daily,
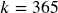 .
.
- If the compounding is done annually (once a year),
The most important thing to remember about using this formula is that it assumes that we put money in the account once and let it sit there earning interest.
Example of Compound Interest
A certificate of deposit (CD) is a savings instrument that many banks offer. It usually gives a higher interest rate, but you cannot access your investment for a specified length of time. Suppose you deposit $3000 in a CD paying 6% interest, compounded monthly. How much will you have in the account after 20 years?
In this example,
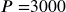 the initial deposit
the initial deposit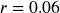 6% annual rate
6% annual rate 12 months in 1 year
12 months in 1 year since we are looking for how much we’ll have after 20 years.
since we are looking for how much we’ll have after 20 years.
So ![]() (round your answer to the nearest penny)
(round your answer to the nearest penny)
Let us compare the amount of money earned from compounding against the amount you would earn from simple interest
| Years | Simple Interest ($15 per month) | 6% compounded monthly = 0.5% each month. |
| 5 | $3900 | $4046.55 |
| 10 | $4800 | $5458.19 |
| 15 | $5700 | $7362.28 |
| 20 | $6600 | $9930.61 |
| 25 | $7500 | $13394.91 |
| 30 | $8400 | $18067.73 |
| 35 | $9300 | $24370.65 |
Example of Compounding for Savings
You know that you will need $40,000 for your child’s education in 18 years. If your account earns 4% compounded quarterly, how much would you need to deposit now to reach your goal?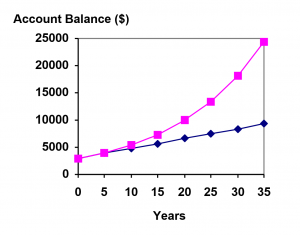
In this example,
We’re looking for P.
![]()
![]()
![]()
![]()
In this case, we’re going to have to set up the equation, and solve for ![]() .
.
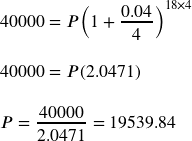
So you would need to deposit $19,539.84 now to have $40,000 in 18 years.
 A note about rounding:
A note about rounding:
It is important to be very careful about rounding when calculating things with exponents. In general, you want to keep as many decimals during calculations as you can. Be sure to keep at least 3 significant digits (numbers after any leading zeros). Rounding 0.00012345 to 0.000123 will usually give you a “close enough” answer, but keeping more digits is always better. If your calculator allows it, do all your calculations without rounding in the calculator and only round the final answer.
To see why not over-rounding is so important, suppose you were investing ![]() P=/
P=/![]()
![]()
![]()
![]()
If we first compute ![]() , we find
, we find ![]()
Here is the effect of rounding this to different values:
| r/k rounded to: | Gives A to be: | Error |
| 0.004 | $4208.59 | $259.15 |
| 0.0042 | $4521.45 | $53.71 |
| 0.00417 | $4473.09 | $5.35 |
| 0.004167 | $4468.28 | $0.54 |
| 0.0041667 | $4467.80 | $0.06 |
| no rounding | $4467.74 |
If you’re working in a bank, of course you wouldn’t round at all. For our purposes, the answer we got by rounding to 0.00417, three significant digits, is close enough – $5 off of $4500 isn’t too bad. Certainly keeping that fourth decimal place wouldn’t have hurt.
Using Technology
In many cases, you can avoid rounding completely by how you enter things in your calculator or Excel. For example, in the example above, we needed to calculate:
![]()
We can quickly calculate 12×30 = 360, giving ![]()
Now we can use the calculator.
For a TI or Casio graphing calculator, we can type:
1000 (1+.05/12)^360
You can also use TVM solver in your Calculator:
In a TI 83/84:
- Use APPS, then hit 1: Finance
- Hit ENTER or 1: TVM Solver
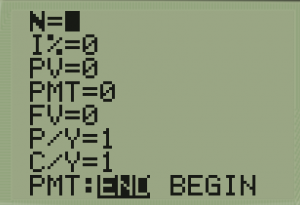
- Fill in the TVM Solver according to our problem leaving blank the one we are solving for:
- N represents
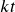 the total number of compounding periods
the total number of compounding periods 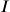 is the interest rate as a percentage
is the interest rate as a percentage- PV = Present Value, or Principal as a negative value…yes this is negative because we are putting the money IN the account AWAY from us
- PMT = 0 This will be changes we make (add or subtract money), leave this = 0 for compound interest
- FV = Future Value, this is our A
- P/Y = Payments per year (we do not have these in compound interest, but we must have a number here, so use
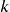 )
) - C/Y – Compounding per year…this is our
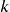
- PMT: End – for the majority of our problems we will keep this on End or the period instead of beginning.
- N represents
- Then go to the variable you want to solve for that you left blank and use the ALPHA button and = button (you will see the word SOLVE in the same color as the alpha button on your calculator. This will fill in the blank with the variable that we left unknown.
Trying this with ![]() for 30 years.
for 30 years.
| We Enter: | After ALPHA = or SOLVE |
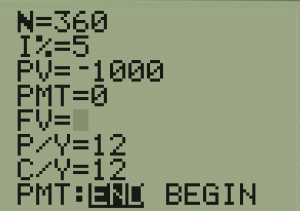 |
 |
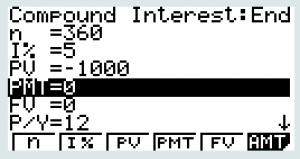
On a CASIO Graphing Calculator:
- Go to MENU and TVM in the lower right side and EXE
- Hit F2 for Compound Interest
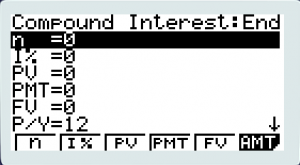
- Fill in the TVM Solver according to our problem leaving blank the one we are solving for:
- n =
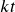 the total number of compound periods
the total number of compound periods 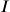 = The rate as a percent
= The rate as a percent- PV = Present Value or Principal
- PMT =0 This will be changes we make (add or subtract money), leave this = 0 for compound interest
- FV = Future Value, this is our A
- P/Y = Payments per year (we do not have these in compound interest, but we must have a number here, so use
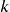 )
) - C/Y – Compounding per year…this is our
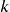
- n =
- Now you can click on the F number corresponding to the variable you would like to solve for.
Trying this with ![]() for 30 years.
for 30 years.
| We Enter: | After Hitting F5 to Solve for FV |
 |
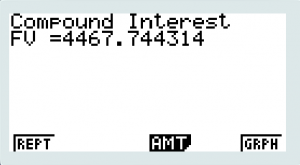 |
In Excel or Google Sheets
In Excel or Google Sheets, there are several commands that figure compound interest:
- =FV(r/k, kt, 0, -P) will provide the A or future value, given the other variables (Note: put the present value or principal in as a negative number)
- =PV(r/k, kt, 0, A) will provide the –P or the negative of the Principal or the Present Value
- =NPER(r/k, 0, -P, A) will give the number of periods necessary to go from the principal to amount needed. This can be divided by k to find the number of years.
- =RATE(kt, 0, -P, A) will give the rate necessary to make A out of P in t years compounding k times a year.
Try in Now 2
If $70,000 are invested at 7% compounded monthly for 25 years, find the end balance.
Because of compounding throughout the year, with compound interest the actual increase in a year is more than the annual percentage rate. If $1,000 were invested at 10%, the table below shows the value after 1 year at different compounding frequencies:
| Frequency | Value after 1 year |
| Annually | $1100 |
| Semiannually | $1102.50 |
| Quarterly | $1103.81 |
| Monthly | $1104.71 |
| Daily | $1105.16 |
If we were to compute the actual percentage increase for the daily compounding, there was an increase of $105.16 from an original amount of $1,000, for a percentage increase of ![]() increase.
increase.
This quantity is called the annual percentage yield (APY).
Notice that given any starting amount, the amount after 1 year would be ![]() . To find the total change, we would subtract the original amount, then to find the percentage change we would divide that by the original amount:
. To find the total change, we would subtract the original amount, then to find the percentage change we would divide that by the original amount:
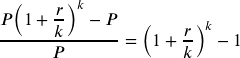
Annual Percentage Yield
The annual percentage yield (also called effective rate) is the actual percent a quantity increases in one year. It can be calculated as
![]()
Notice this is equivalent to finding the value of $1 after 1 year, and subtracting the original dollar.
Examples of APY
Bank A offers an account paying 1.2% compounded quarterly. Bank B offers an account paying 1.1% compounded monthly. Which is offering a better rate?
We can compare these rates using the annual percentage yield – the actual percent increase in a year.
Bank A: ![]()
Bank B: ![]()
Bank B’s monthly compounding is not enough to catch up with Bank A’s better APR. Bank A offers a better rate.
Calculators and Excel also have a functions for calculating APY or effective rate.
On a TI 83/84 Model:
- Push APPS and 1 or ENTER for Finance
- Scroll Down until you see a triangle and Eff (This stands for Effective Rate)
- Click ENTER on Eff
- You will have a triangle Eff( on your screen, type in the rate as a percent and comma (above the 7) the number of compounds per year,
 and enter and you will have the APY
and enter and you will have the APY
For the previous example: it would be Eff(1.2,4) for bank A and Eff(1.1, 12) for bank B
On a CASIO graphing calculator:
- Go to Menu and move to TVM and hit EXE
- Click F5 for CNVT (Conversion)
- For n, put in your k instead (number of compounding periods per year)
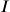 = APR as the percent
= APR as the percent- Click F1 for EFF
In Excel:
- The command is =EFFECT(r, k)
- This one is in decimal form or percent if you actually type in the % sign, but the answer will be in a decimal unless you format the cell to be in percent form.
Try it Now 3
What is the APY or effective rate for a CD that pays 2.5% interest compounding monthly?
Example of Doubling
If you invest $2000 at 6% compounded monthly, how long will it take the account to double in value?
This is a compound interest problem, since we are depositing money once and allowing it to grow. In this problem,
![]()
![]()
![]()
So our general equation is ![]() . We also know that we want our ending amount to be double of $2000, which is $4000, so we’re looking for
. We also know that we want our ending amount to be double of $2000, which is $4000, so we’re looking for ![]() so that
so that ![]() . To solve this, we set our equation for
. To solve this, we set our equation for ![]() equal to $4000.
equal to $4000.
![]()
Divide both sides by 2000
![]()
Take logs of both sides:
![]()
Use Exponent Property of logs on the right side:
![]()
Divide both sides by ![]() :
:
![]()
![]()
It will take about 11.581 years for the account to double in value. Note that your answer may come out slightly differently if you had evaluated the logs to decimals and rounded during your calculations, but your answer should be close. For example if you rounded log(2) to 0.301 and log(1.005) to 0.00217, then your final answer would have been about 11.577 years.
Try it Now Answers
-
- I = $30 of interest
P = $500 principal
r = unknown
t = 1 monthUsing I = Prt, we get 30 = 500·r·1. Solving, we get r = 0.06, or 6%. Since the time was monthly, this is the monthly interest. The annual rate would be 12 times this: 72% interest. 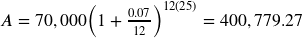
- 2.5288%
- I = $30 of interest
Media Attributions
- 81example1
- takenote is licensed under a Public Domain license
- TVMsolver
- 81example2
- 81example3
- 81example4
- 81example5
- 81example6

