6.2 Rational Equations
Solving Rational Equations that Reduce to Linear Equations
In this section, we look at rational equations that, after some manipulation, result in a linear equation. If an equation contains at least one rational expression, it is a considered a rational equation.
Rational equations have a variable in the denominator in at least one of the terms. Our goal is to perform algebraic operations so that the variables appear in the numerator. In fact, we will eliminate all denominators by multiplying both sides of the equation by the least common denominator (LCD).
Finding the LCD is identifying an expression that contains the highest power of all of the factors in all of the denominators. We do this because when the equation is multiplied by the LCD, the common factors in the LCD and in each denominator will equal one and will cancel out.
Rational Equations and how to solve them
A rational equation contains at least one rational expression where the variable appears in at least one of the denominators. They can be solved as follows:
- If there is only one term on each side, cross multiply OR
- If not, factor all denominators in the equation.
- Find the LCD.
- Multiply both sides of the equation by the LCD. If the LCD was correct, there should be no denominators left.
- Solve the remaining equation.
- Make sure to check solutions back in the original equations to avoid a solution producing zero in a denominator.
 Note that any solution that makes a denominator in the original expression equal zero must be excluded from the possibilities. This is something we always need to check for.
Note that any solution that makes a denominator in the original expression equal zero must be excluded from the possibilities. This is something we always need to check for.
Example Solving a Rational Equation
Solve the rational equation: ![]() .
.
We have three denominators ![]() and 3. The LCD must contain
and 3. The LCD must contain ![]() and 3. An LCD of
and 3. An LCD of ![]() contains all three denominators. In other words, each denominator can be divided evenly into the LCD. Next, multiply both sides of the equation by the LCD
contains all three denominators. In other words, each denominator can be divided evenly into the LCD. Next, multiply both sides of the equation by the LCD![]() .
.
![]()
Distribute:
![]()
![]()
![]()
![]()
A common mistake made when solving rational equations involves finding the LCD when one of the denominators is a binomial—two terms added or subtracted—such as ![]() . Always consider a binomial as an individual factor; the terms cannot be separated. For example, suppose a problem has three terms and the denominators are
. Always consider a binomial as an individual factor; the terms cannot be separated. For example, suppose a problem has three terms and the denominators are ![]() and
and ![]() . First, factor all denominators. We then have
. First, factor all denominators. We then have ![]() and
and ![]() as the denominators. (Note the parentheses placed around the second denominator.) Only the last two denominators have a common factor of
as the denominators. (Note the parentheses placed around the second denominator.) Only the last two denominators have a common factor of ![]() . The
. The ![]() in the first denominator is separate from the
in the first denominator is separate from the ![]() in the
in the ![]() denominators. An effective way to remember this is to write factored and binomial denominators in parentheses, and consider each parentheses as a separate unit or separate factor. The LCD in this instance is found my multiplying together the
denominators. An effective way to remember this is to write factored and binomial denominators in parentheses, and consider each parentheses as a separate unit or separate factor. The LCD in this instance is found my multiplying together the ![]() , one factor of
, one factor of ![]() , and the
, and the ![]() . Thus the LCD is the following:
. Thus the LCD is the following:
![]()
So, both sides of the equation would be multiplied by ![]() . Leave the LCD in factored form, as this makes it easier to see how each denominator in the problem cancels out.
. Leave the LCD in factored form, as this makes it easier to see how each denominator in the problem cancels out.
Another example is a problem with two denominators, such as ![]() and
and ![]() . Once the second denominator is factored as
. Once the second denominator is factored as ![]() , there is a common factor of
, there is a common factor of ![]() in both denominators and the LCD is
in both denominators and the LCD is ![]() .
.
Sometimes we have a rational equation in the form of a proportion; that is, when one fraction equals another fraction and there are no other terms in the equation.
![]()
We can then use another method of solving the equation, without find the LCD: cross-multiplication. We multiply terms by crossing over the equal sign.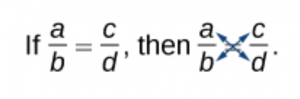
So this results is ![]() .
.
Example Solving a Rational Equation Using Cross Multiplication
Solve the following rational equation:
![]()
Cross Multiplying gives us:
![]()
![]()
![]()
![]()
Since the only number that would make a denominator 0 would be 0 itself, we have our solution.
Try it Now 1
Example Solving a Rational Function with no factoring necessary
Solve the following rational equations:
a. ![]()
Our denominators are ![]() and
and ![]() , so our LCD is
, so our LCD is ![]() .
.
Multiply everything by ![]() :
:
![]()
Distribute:
![]()
Cancel and multiply leftovers:
![]()
![]()
![]()
This does not make any denominator 0, so our solutions is ![]() .
.
Try it Now 2
Solve the rational equation: ![]() .
.
Example Solving a Rational Equation by Factoring the Denominator
Solve the rational equation: ![]() .
.
Let’s look at all the denominators in their factored form: ![]() List all the factors that appear:
List all the factors that appear: ![]() and
and ![]() So the LCD must be
So the LCD must be ![]() . Multiply both sides by
. Multiply both sides by ![]() :
:
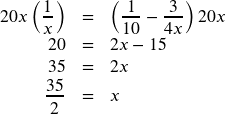
Since this does not make the denominator 0, our solution is ![]() .
.
Try it Now 3
Solve the rational equation: ![]() .
.
Examples Solving Rational Equations with a Binomial in the Denominator
a. Solve and state the excluded values: ![]()
This one can be cross-multiplied
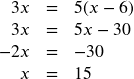
The solution is 15, and the excluded values are 6, 0.
b. Solve and state the excluded values: ![]()
The LCD is ![]() . Multiply both sides of the equation by
. Multiply both sides of the equation by ![]()
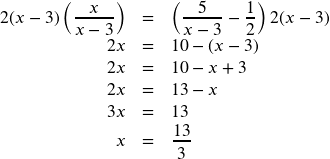
The solution is ![]() . The excluded value is 3.
. The excluded value is 3.
c. Solve and state the excluded values: ![]()
The LCD is ![]() . Multiply both sides of the equation by
. Multiply both sides of the equation by ![]()
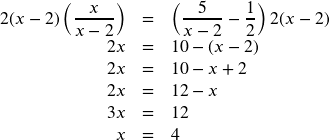
The solution is 4. The excluded value is 3.
Try it Now 4
Solve and state the excluded values: ![]()
Example Solving a Rational Equation with Factored Denominators and Stating Excluded Values
Solve the rational equation after factoring the denominators and state the excluded values:
![]()
The first two denominators are already factored as far as possible, ![]() and
and ![]() , but the third one
, but the third one ![]() can be factored as difference of two squares:
can be factored as difference of two squares: ![]() . Thus, the LCD that contains each denominator is
. Thus, the LCD that contains each denominator is ![]() . Multiply the whole equation by the LCD, cancel out the denominators, and solve the remaining equation.
. Multiply the whole equation by the LCD, cancel out the denominators, and solve the remaining equation.
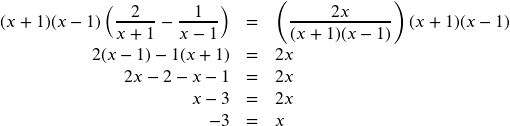
The solution is -3. The excluded values are 1 and -1.
Try it Now 5
Solve the rational equation and state the excluded values:
![]() .
.
Solving Rational Equations Resulting in a Quadratic
Sometimes, solving a rational equation results in a quadratic. When this happens, we continue the solution by simplifying the quadratic equation by one of the methods we have seen. It may turn out there is no solution.
Example Solving a Rational Equation Leading to a Quadratic
Solve the rational equation and state the excluded values:
![]() .
.
Similar to the previous example, the LCD is ![]() so we will multiply both sides by
so we will multiply both sides by ![]() :
:
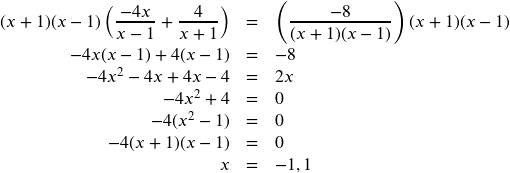
Now we have a problem, because the solution -1 and 1 is the same as our excluded values since they make the original denominators equal to 0 and therefore there is no solution.
 Note with rational equations that lead to quadratics, you can have 0, 1 or 2 solutions. You can solve and get 1 solution that is excluded and 1 that is not or you can get both solutions that work in the equation as well.
Note with rational equations that lead to quadratics, you can have 0, 1 or 2 solutions. You can solve and get 1 solution that is excluded and 1 that is not or you can get both solutions that work in the equation as well.
Try it Now 6
Solve the rational equation and state the excluded values:
![]() .
.
Try it Now Answers
- Cross Multiply. Solution:
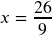 Exclusions: -6 and 2/3
Exclusions: -6 and 2/3 - LCD:
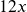 ; Solution:
; Solution: 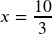 ; Exclusion: 0
; Exclusion: 0 - LCD:
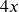 ; Solution:
; Solution: 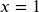 ; Exclusion: 0
; Exclusion: 0 - Cross Multiply. Solution:
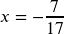 ; Exclusions -1/2 and -1/3
; Exclusions -1/2 and -1/3 - LCD:
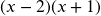 ; Solution:
; Solution: 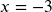 ; Exclusions 2 and -1
; Exclusions 2 and -1 - LCD:
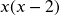 ; Solution:
; Solution: 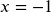 ; Exclusions 0, 2 (Note that the quadratic produced solutions of -1 and 0, but since 0 was on the exclusion list it cannot be a solution.)
; Exclusions 0, 2 (Note that the quadratic produced solutions of -1 and 0, but since 0 was on the exclusion list it cannot be a solution.)
Media Attributions
- warningsign
- crossmult
- takenote is licensed under a Public Domain license

