1.1 Exponents and Scientific Notation
Review of Intermediate Algebra
Mathematicians, scientists, economists and other professionals commonly encounter very large and very small numbers. However, it may not be obvious how common values like these are in everyday life. For instance, a pixel is the smallest unit of light that can be perceived and recorded by a digital camera. A particular camera might record an image that is 2,048 pixels by 1,536 pixels, which is a very high-resolution picture. It can also perceive a color depth (gradations in colors) of up to 48 bits per frame and can shoot the equivalent of 24 frames per second. The maximum possible number of bits of information used to film a one-hour (3,600-second) digital film is then an extremely large number.
Using a calculator, we enter 2,048 × 1,536 × 48 × 24 × 3,600 and press ENTER. The calculator displays 1.304596316E13. What does this mean? The “E13” portion of the result represents the exponent 13 of ten, so there are a maximum of approximately 1.3×1013 bits of data in that one-hour film. In this section, we review rules of exponents first and then apply them to calculations involving very large or small numbers.
Using the Product Rule of Exponents
Consider the product ![]() Both terms have the same base,
Both terms have the same base, ![]() , but they are raised to different exponents. Expand each expression, and then rewrite the resulting expression.
, but they are raised to different exponents. Expand each expression, and then rewrite the resulting expression.
![Rendered by QuickLaTeX.com \[\begin{array}{l} \mathop {\left( {x \cdot x \cdot x} \right)}\limits^{\text{3 \emph{factors}}} \cdot \mathop {\left( {x \cdot x \cdot x \cdot x} \right)}\limits^{\text{4 \emph{factors}}}\\ \quad \quad \;\; = \mathop {x \cdot x \cdot x \cdot x \cdot x \cdot x \cdot x}\limits^{\text{7 \emph{factors}}}\\ \quad \quad \;\; = {x^7} \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-51fa619ce3b00435e9d48f3e5a99fc5c_l3.png)
The result is that ![]() .
.
Notice that the exponent of the product is the sum of the exponents of the factors. In other words, when multiplying exponential expressions with the same base, we write the result with the common base and add the exponents. This is the product rule of exponents.
Product Rule of Exponents
For any real number a and natural numbers m and n, the product rule of exponents states that:
![]()
Now consider an example with real numbers.
![]()
We can always check that this is true by simplifying each exponential expression. We find that ![]() and
and ![]() The product
The product ![]() so the relationship is true. We can use the product rule of exponents to simplify expressions that are a product of two numbers or expressions with the same base but different exponents. We can even use the product rule of exponents with integers as well, as seen in example c below.
so the relationship is true. We can use the product rule of exponents to simplify expressions that are a product of two numbers or expressions with the same base but different exponents. We can even use the product rule of exponents with integers as well, as seen in example c below.
Examples Using the Product Rule of Exponents
a. ![]()
Here, we would just add the exponents:
![]()
b. ![]()
This seems complicated because of the negative, but again, once we add the exponents, this would become positive due to the even exponent. (Note that when we do not see an exponent, we assume that it is 1.)
![]()
c. ![]()
At first, we may think we cannot simplify a product of three factors, but using the associative properties of multiplication and addition, we can simply add all three exponents. Since the 3 is negative, we add a negative 3, which is the same as subtracting 3.
![]()
Try it Now 1
a. ![]()
b. ![]()
c. ![]()
See Try it Now answers at the end of each section.
Using the Quotient Rule of Exponents
The quotient rule of exponents allows us to simplify an expression that divides two numbers with the same base. In a similar way to the product rule, we can simplify an expression such as ![]() . Consider the example
. Consider the example ![]() . What happens if we write this out:
. What happens if we write this out:
![Rendered by QuickLaTeX.com \[\begin{array}{l} \dfrac{{{y^6}}}{{{y^2}}} = \dfrac{{y \cdot y \cdot y \cdot y \cdot y \cdot y}}{{y \cdot y}}\\ \quad \; = \dfrac{{ \cancel{y}\cdot \cancel{y} \cdot y \cdot y \cdot y \cdot y}}{{ \cancel{y}\cdot \cancel{y}}}\\ \quad \; = \dfrac{{y \cdot y \cdot y \cdot y}}{1} = {y^4} \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6dcd88cc132daa3a1123c09e0283f9f3_l3.png)
When dividing exponential expressions with the same base, we write the result with the common base and subtract the exponents.
![]()
Quotient Rule for Exponents
For any nonzero real number ![]() and natural numbers
and natural numbers ![]() and
and ![]() , the quotient rule of exponents states that
, the quotient rule of exponents states that
![]()
Examples using the Quotient Rule of Exponents
a. ![]()
Here, we can just subtract the exponents: ![]()
b. ![]()
This might look difficult, but again, a simple subtraction: ![]()
c. 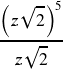
We begin with the quotient rules of exponents: ![]() (this can be simplified further so we will revisit it later)
(this can be simplified further so we will revisit it later)
Try it Now 2
a. ![]()
b. ![]()
c. ![]()
Using the Power Rule of Exponents
Suppose an exponential expression is raised to some power. Can we simplify the result? Yes. To do this, we use the power rule of exponents. Consider the expression ![]() . If we break up the outside exponent, it means that
. If we break up the outside exponent, it means that ![]() is multiplied to itself twice, but as we’ve seen above with the Product Rule, we can add the exponents. And note that repeated addition is just multiplication.
is multiplied to itself twice, but as we’ve seen above with the Product Rule, we can add the exponents. And note that repeated addition is just multiplication.
![]()
The exponent of the answer is the product of the exponents: ![]() In other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents.
In other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents.
The Power Rule of Exponents
For any real number![]() and positive integers
and positive integers ![]() and
and ![]() , the power rule of exponents states that:
, the power rule of exponents states that:
![]()
Be careful to distinguish between uses of the product rule and the power rule. When using the product rule, different terms with the same bases are raised to exponents. In this case, you add the exponents. When using the power rule, a term in exponential notation is raised to a power. In this case, you multiply the exponents.
| Product Rule | Power Rule | |||||
| but | ||||||
| but | ||||||
| but |
Examples using the Power Rule of exponents
a. ![]()
Just multiply the exponents: ![]()
b. ![]()
Again, we just multiply the exponents but make sure we keep the parenthesis around 2t so that we remember that the exponent applies to both 2 and t.
![]()
c. ![]()
![]()
But, does it really still have to be negative? Remember a negative number to an even power is positive! So we can call this ![]() which is a really large number!
which is a really large number!
Try It Now 3
a. ![]()
b. ![]()
c. ![]()
Using the Zero Exponent Rule of Exponents
Return to the quotient rule. What would happen if ![]() . In this case, we would use the zero exponent rule of exponents to simplify the expression to 1. To see how this is done, let us begin with an example.
. In this case, we would use the zero exponent rule of exponents to simplify the expression to 1. To see how this is done, let us begin with an example.
![]()
If we were to simplify the original expression using the quotient rule, we would have:
![]()
If we take the two answers equal to each other, we would have ![]() . This is true for any non-zero real number base or a variable that represents a non-zero real number. The exception is
. This is true for any non-zero real number base or a variable that represents a non-zero real number. The exception is ![]() . This is an indeterminate form.
. This is an indeterminate form.
Zero Exponent Rule
For any nonzero real number ![]() , the zero exponent rule of exponents states that:
, the zero exponent rule of exponents states that:
![]()
Examples Using the Zero Exponent Rule
a. ![]()
![]()
b. ![]()
The -3 here just comes along for the ride: ![]()
c. 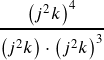
This will take two steps, first we can use the addition rule for the denominator:
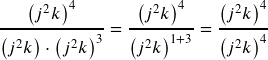
Now we apply the zero exponent rule:
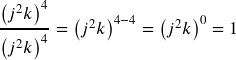
Try It Now 4
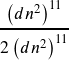
Using the Negative Rule of Exponents
All our previous examples in the quotient rule had the exponent in the numerator larger than the denominator. In the zero exponent rule, we investigated what happened when the exponents in the numerator and denominator were equal. Another useful result occurs if we consider what happens when ![]() . For example, can we simplify
. For example, can we simplify ![]() ?
?
Use our example, ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{array}{l} \dfrac{h^3}{h^5} = \dfrac{h \cdot h \cdot h}{h \cdot h \cdot h \cdot h \cdot h}\\ \quad \; = \dfrac{ \cancel{h} \cdot \cancel{h} \cdot \cancel{h}}{ \cancel{h} \cdot \cancel{h} \cdot \cancel{h} \cdot h \cdot h}\\ \quad \; = \dfrac{1}{h \cdot h} = \dfrac{1}{h^2} \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-920b5e092393c281d02ad28647dfecab_l3.png)
If we were to simplify the original expression using the quotient rule, we would have
![]()
Putting the answers together, we have ![]() . This is true for any nonzero real number, or any variable representing a nonzero real number. Why do we have to say “nonzero?” Because we cannot have 0 in the denominator of a fraction.
. This is true for any nonzero real number, or any variable representing a nonzero real number. Why do we have to say “nonzero?” Because we cannot have 0 in the denominator of a fraction. ![]() is undefined.
is undefined.
A factor with a negative exponent becomes the same factor with a positive exponent if it is moved across the fraction bar—from numerator to denominator or vice versa.
![]()
We have shown that the exponential expression ![]() is defined when
is defined when ![]() is a natural number, 0, or the negative of a natural number. That means that
is a natural number, 0, or the negative of a natural number. That means that ![]() is defined for any integer
is defined for any integer ![]() . Also, the product and quotient rules and all of the rules we will look at soon hold for any integer
. Also, the product and quotient rules and all of the rules we will look at soon hold for any integer ![]() .
.
The Negative Rule of Exponents
For any nonzero real number![]() and natural number
and natural number ![]() the negative rule of exponents states that
the negative rule of exponents states that
![]()
Examples Using the Quotient Rule with the Negative Exponent Rule
a. ![]()
Just subtract the exponents: ![]()
Now use the negative exponent rule to make this a positive exponent: ![]()
b. ![]()
We start by combining the two bases in the numerator using the product rule: ![]()
Now we use the quotient rule: ![]()
Now we use negative exponent rule: ![]()
c. 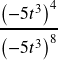
Use our quotient rule and negative exponent rule:
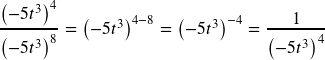
Try it Now 5
a. ![]()
b. ![]()
c. ![]()
Examples using the Product and Quotient Rules and the Zero and Negative Exponent Rule
a. ![]()
Start with the product rule: ![]()
Now the negative exponent rule: ![]()
b. ![]()
![]()
c. ![]()
Perform the quotient rule:
![]()
Try it Now 6
a. ![]()
b. ![]()
Find the Power of a Product
To simplify the power of a product of two exponential expressions, we can use the power of a product rule of exponents, which breaks up the power of a product of factors into the product of the powers of the factors. For instance, consider ![]() We begin by using the associative and commutative properties of multiplication to regroup the factors.
We begin by using the associative and commutative properties of multiplication to regroup the factors.
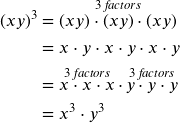
 Warning! This does not work when there is a + or – in the ( )!
Warning! This does not work when there is a + or – in the ( )! ![]() but
but ![]() . More on this in the next section.
. More on this in the next section.
Power of a Product Rule of Exponents
For any real numbers ![]() and
and ![]() and any integer
and any integer ![]() the power of a product rule of exponents states that
the power of a product rule of exponents states that
![]()
Examples for finding the power of a product
a. ![]()
First use the power of product rule: ![]()
Now we apply the power rule of exponents:
![]()
b. ![]()
![]() (Using a calculator, press 2 ^ 15)
(Using a calculator, press 2 ^ 15)
c. ![]()
![]()
d. ![]()
![]()
e. ![]()
![]()
But note we have a negative exponent here so putting that into the denominator, we end up with ![]() .
.
Try It Now 7
a. ![]()
b. ![]()
c. ![]()
d. ![]()
e. ![]()
Finding the Power of a Quotient
To simplify the power of a quotient of two expressions, we can use the power of a quotient rule, which states that the power of a quotient of factors is the quotient of the powers of the factors. For example, let’s look at part e in the examples above.
![]()
What if we started by rewriting the original problem using the Negative Rule of Exponents:
![]()
It appears from the last two steps that we can use the power of a product rule as a power of a quotient rule.
![Rendered by QuickLaTeX.com \[\begin{array}{l} {\left( {{p^{ - 2}}{q^2}} \right)^7} = {\left( {\dfrac{{{q^2}}}{{{p^2}}}} \right)^7}\\ \quad \quad \quad \;\;\; = \dfrac{{{{\left( {{q^2}} \right)}^7}}}{{{{\left( {{p^2}} \right)}^7}}}\\ \quad \quad \quad \;\;\; = \dfrac{{{q^{2 \cdot 7}}}}{{{p^{2 \cdot 7}}}}\\ \quad \quad \quad \;\;\; = \dfrac{{{q^{14}}}}{{{p^{14}}}} \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d0d5fd3589d87d96beecc418a8dc3483_l3.png)
The Power of a Quotient Rule of Exponents
For any real number ![]() and nonzero real number
and nonzero real number ![]() and any integer
and any integer ![]() , the power of a quotient rule of exponents states that
, the power of a quotient rule of exponents states that
![]()
Examples using the power of a quotient rule
a. ![]()
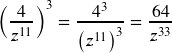
b. ![]()
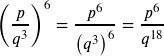
c. ![]()
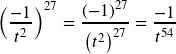
d. ![]()
![]()
e. ![]()
![]()
Try it Now 8
a. ![]()
b. ![]()
c. ![]()
d. ![]()
e. ![]()
Simplifying Exponential Expressions
Recall that to simplify an expression means to rewrite it by combing terms or exponents; in other words, to write the expression more simply with fewer terms. The rules for exponents may be combined to simplify expressions.
Examples simplifying exponential expressions
Simplify each expression and write the answer with positive exponents only (assume variables represent nonzero real numbers.)
a. ![]()
- Apply Power of a Product:
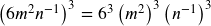
- Using Power Rule of exponents:
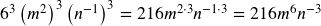
- Now apply the Negative Exponent Rule:
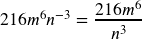
b. ![]()
- Product Rule:
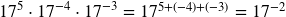
- Negative Exponent Rule:
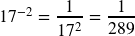
c. ![]()
- Power of a product and quotient:
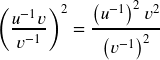
- Power Rule:
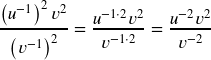
- Negative Exponent Rule:
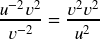
- Product Rule:
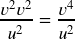
d. ![]()
Multiply constants and using the product rule:
![]()
e. ![]()
- Use the product rule:
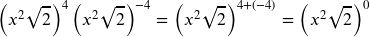
- Use zero exponent rule:
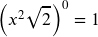
f. 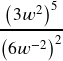
- Notice that the 6 could be written as
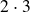 and then use power rule:
and then use power rule: 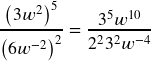
- Now the Quotient Rule:
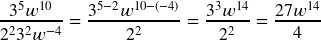
Try It Now 9
Simplify each expression and write the answer with positive exponents only (assume variables represent nonzero real numbers.)
a. ![]()
b. ![]()
c. ![]()
d. ![]()
e. ![]()
f. 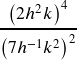
Using Scientific Notation
Recall at the beginning of the section that we found the number ![]() when describing bits of information in digital images. Other extreme numbers include the width of a human hair, which is about 0.00005 m, and the radius of an electron, which is about 0.00000000000047 m. How can we effectively work read, compare, and calculate with numbers such as these?
when describing bits of information in digital images. Other extreme numbers include the width of a human hair, which is about 0.00005 m, and the radius of an electron, which is about 0.00000000000047 m. How can we effectively work read, compare, and calculate with numbers such as these?
A shorthand method of writing very small and very large numbers is called scientific notation, in which we express numbers in terms of exponents of 10. To write a number in scientific notation, move the decimal point to the right of the first digit in the number. Write the digits as a decimal number between 1 and 10. Count the number of places ![]() that you moved the decimal point. Multiply the decimal number by 10 raised to a power of
that you moved the decimal point. Multiply the decimal number by 10 raised to a power of ![]() . If you moved the decimal left as in a very large number,
. If you moved the decimal left as in a very large number, ![]() is positive. If you moved the decimal right as in a small large number,
is positive. If you moved the decimal right as in a small large number, ![]() is negative.
is negative.
For example, consider the number 2,780,418. Move the decimal left until it is to the right of the first nonzero digit, which is 2.
![Rendered by QuickLaTeX.com \[ 2.\underbrace{\decposl{7}\decposl{8}\decposl{0}\decposl{4}\decposl{1}\decposl{8.}}_{\textsf{6 places}}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5edf9fd71652a94b92191c145ec3cef1_l3.png)
We obtain 2.780418 by moving the decimal point 6 places to the left. Therefore, the exponent of 10 is 6, and it is positive because we moved the decimal point to the left. This is what we should expect for a large number.
![]()
We often round to a few significant digits, which means the number of digits once a number is in scientific notation. ![]() would be 3 significant digits,
would be 3 significant digits, ![]() would be 2 significant digits.
would be 2 significant digits.
Working with small numbers is similar. Take, for example, the radius of an electron, 0.00000000000047 m. Perform the same series of steps as above, except move the decimal point to the right.
![Rendered by QuickLaTeX.com \[ 0.\underbrace{\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{4.}}_{\textsf{13 places}} 7\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-748e57afccbe8b060c04d5678a38a8cd_l3.png)
Be careful not to include the leading 0 in your count. We move the decimal point 13 places to the right, so the exponent of 10 is 13. The exponent is negative because we moved the decimal point to the right. This is what we should expect for a small number.
![]()
This number has 2 significant digits.
Scientific Notation
A number is written in scientific notation if it is written in the form ![]() , where
, where ![]() and
and ![]() is an integer.
is an integer.
The number of digits in ![]() is called the significant digits.
is called the significant digits.
Examples of Converting Standard Notation to Scientific Notation (and rounded to 4 significant digits)
a. The gross domestic product (GDP) of the US in 2019 was 21,440,000,000,000 US Dollars.
Let’s see how many decimal places we have to move to get one digit to the left of the decimal:
![Rendered by QuickLaTeX.com \[ 2.\underbrace{\decposl{1}\decposl{4}\decposl{4}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0.}}_{\textsf{13 places}}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1a5ed0c59b3cdbc31b5fae75a3d81711_l3.png)
It’s 13 so it’s ![]() .
.
b. The gross national product (GNP) of India in 2019 was 145,229,310,000,000 Indian Rupees.
![Rendered by QuickLaTeX.com \[ 1.\underbrace{\decposl{4}\decposl{5}\decposl{2}\decposl{2}\decposl{9}\decposl{3}\decposl{1}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0.}}_{\textsf{14 places}}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e47d819ce06262e583f43c4b07f36419_l3.png)
It’s 14 so it’s ![]() . But if we round to 4 significant digits, it will be
. But if we round to 4 significant digits, it will be ![]() .
.
c. The Uzbekistan So’m is worth 0.00009868 US Dollars.
![Rendered by QuickLaTeX.com \[ 0.\underbrace{\deci{0}\deci{0}\deci{0}\deci{0}\deci{9.}}_{\textsf{5 places}} 868\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-abe72a17bbde2d90995532ce1400ba15_l3.png)
We went 5 places to the right, so our exponent is ![]() and the number in scientific notation becomes
and the number in scientific notation becomes ![]()
d. The chances of winning a PowerBall lottery is about 0.00000000342466.
![Rendered by QuickLaTeX.com \[ 0.\underbrace{\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{3.}}_{\textsf{9 places}} 42466\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e002043a7e4f50f1484d99e6e5485133_l3.png)
9 places to the right, so our exponent is ![]() and our value is
and our value is ![]() , but if we round off to 4 significant digits, it would be
, but if we round off to 4 significant digits, it would be ![]() Note that it rounds up to 5 because the next digit is 5 or greater.
Note that it rounds up to 5 because the next digit is 5 or greater.
 If the given number is greater than 1, as in examples a–b the exponent of 10 is positive; and if the number is less than 1, as in examples c-d, the exponent is negative.
If the given number is greater than 1, as in examples a–b the exponent of 10 is positive; and if the number is less than 1, as in examples c-d, the exponent is negative.
Try it Now 10
a. The gross national product (GNP) of the US in 2019 was 22,040,000,000,000 US Dollars.
b. The gross national product (GDP) of Japan in 2019 was 553,723,600,000,000 Japanese Yen.
c. The South Korean Won is worth 0.000823 US Dollars.
d. The chances of being killed in a shark attack is 0.0000000037864.
Converting from Scientific to Standard Notation
To convert a number in scientific notation to standard notation, simply reverse the process. Move the decimal ![]() places to the right if
places to the right if ![]() is positive or
is positive or ![]() places to the left if
places to the left if ![]() is negative and add zeros as needed. Remember, if
is negative and add zeros as needed. Remember, if ![]() is positive, the value of the number is greater than 1, and if
is positive, the value of the number is greater than 1, and if ![]() is negative, the value of the number is less than one.
is negative, the value of the number is less than one.
Calculators will often given answers in scientific notation especially any number less than 0.001 or larger than 9,999,999,999. In the calculator, we often see the ![]() part of the number and then an E and then the exponent on 10. You will not see the 10. For example, you will see 4.3245318E12 to indicate
part of the number and then an E and then the exponent on 10. You will not see the 10. For example, you will see 4.3245318E12 to indicate ![]() or 1.27915E-5 to indicate
or 1.27915E-5 to indicate ![]() .
.
Examples on Converting Scientific Notation to Standard Notation
a. ![]()
Move the decimal to the right 14 times filling in 0’s where you need them:
![Rendered by QuickLaTeX.com \[ 3.\underbrace{\deci{5}\deci{4}\deci{7}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0.}}_{\textsf{14 places}} \]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2e2b4b07c1cc60ed74acf1af01b24653_l3.png)
= 354,700,000,000,000 (I filled in the commas to see this easier.)
b. -2E6
This is calculator for ![]() and the negative here just stays in the front, and we move the decimal place to the right 6 times.
and the negative here just stays in the front, and we move the decimal place to the right 6 times.
![Rendered by QuickLaTeX.com \[ -2.\underbrace{\deci{0}\deci{0}\deci{0}\deci{0}\deci{0}\deci{0.}}_{\textsf{6 places}} \]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-35d243ea168967fe81cd916f4744ba5c_l3.png)
= -2,000,000
c. 7.91E-7
Again, we have the calculator output style here. So this means we move the decimal point 7 places to the left since it’s ![]()
![Rendered by QuickLaTeX.com \[ 0.\underbrace{\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{7.}}_{\textsf{7 places}}91\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b3249b10350dd830563a90425c32786d_l3.png)
=0.000000791
d. ![]()
Since our exponent is negative, this means 12 places to the left. The negative on the 8 just goes to the front.
![Rendered by QuickLaTeX.com \[ -0.\underbrace{\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{0}\decposl{8.}}_{\textsf{12 places}}05\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1adb3f8277f9d3b76ed0ed09beead17c_l3.png)
=-0.00000000000805
Try it Now 11
a. ![]()
b. -8.16E11
c. 8E6
d. ![]()
-
-
-
-
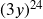
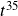
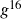 (the negative disappears because it’s inside the parenthesis with an even exponent)
(the negative disappears because it’s inside the parenthesis with an even exponent)
-
- 1

- 1
-
-
-
-
-
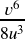
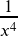
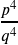
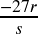
- 1
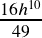
10. a. ![]()
b. ![]()
c. ![]()
d.![]()
11. a. 703,000
b. -816,000,000,000
c. 8,000,000
d. -0.00000000000039
Media Attributions
- warningsign
- takenote is licensed under a Public Domain license

