6.4 Radical Functions and Equations
Along with radical functions and equations, we must also consider rational exponents.
Recall that ![]() In general,
In general, ![]() .
.
In fact we can go even further and look at ![]() . Remember that
. Remember that ![]() So it would would be reasonable to say that
So it would would be reasonable to say that ![]() or
or ![]() .
.
Rational Exponents
For any number ![]() in the domain and non-zero
in the domain and non-zero ![]() :
:
![]()
When we talk about a radical function, we can also consider rational exponent functions as well: ![]() is equivalent to
is equivalent to ![]() We can also consider functions like
We can also consider functions like ![]() .
.
The following graphs show several different radical and rational exponent functions:
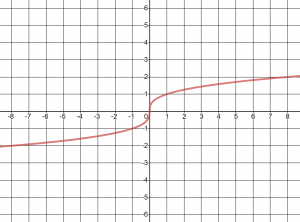
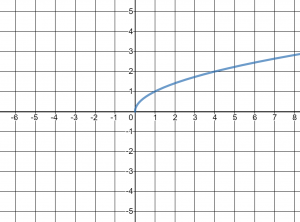
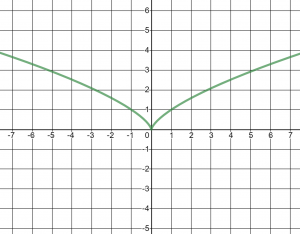
Notice that the domain of ![]() is
is ![]() while the domain of
while the domain of ![]() is
is ![]() We can find the cube roots of negative numbers, and in fact we can find the nth root of any negative number when n is odd. When n is even however, the domain will be restricted to whatever is under the square root sign being greater than zero.
We can find the cube roots of negative numbers, and in fact we can find the nth root of any negative number when n is odd. When n is even however, the domain will be restricted to whatever is under the square root sign being greater than zero.
Examples Finding the Domain of Radical and Rational Exponent Functions
Find the domain of:
a. ![]()
Since this is an even root, we need to make sure what is under the radical is non-negative so the domain would be where ![]() or
or ![]()
b. ![]()
Since the rational exponent has an odd number in the denominator, the domain is unrestricted so the domain is ![]()
Solving Rational Exponent Equations
When we are solving equations, we want to isolate the variable, ![]() . Consider
. Consider ![]() If we take both sides to the power
If we take both sides to the power ![]() then we will undo the 1/2 power:
then we will undo the 1/2 power:
![]()
![]()
![]() so
so ![]()
Solving Equations with Rational Exponents
- Isolate the expression that is taken to the rational exponent
- Take both sides to the power of the reciprocal of that exponent
- Solve the resulting equation
- ALWAYS check for extraneous solutions
 This method can result in solutions that do not actually make the equation true, these are called extraneous solutions. For this reason, it is important to always check your answers in the original equation.
This method can result in solutions that do not actually make the equation true, these are called extraneous solutions. For this reason, it is important to always check your answers in the original equation.
Example Solving an Equation in which a Variable is Raised to a Rational Exponent
a. Solve the equation: ![]() .
.
![]()
Take both sides to the ![]() power:
power:
![]()
![]()
Remember that ![]() is
is ![]()
So ![]()
b. Solve the equation ![]()
This equation involves rational exponents as well as factoring rational exponents. First, put the variable terms on one side of the equation and 0 on the other.
![]()
Now we want to factor out something, so lets factor out the lowest exponent.
![]()
Where did the ![]() come from?
come from?
Consider:
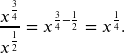
Now, we have ![]() so:
so:
![]() or
or ![]()
So ![]() or
or ![]()
We take the second one to the 4th power:
![]() or
or ![]()
Try it Now 1
a. Solve the equation ![]()
b. Solve the equation ![]()
Solving Radical Equations
Radical equations are equations that contain variables in the radicand (the expression under a radical symbol), such as
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} \sqrt{3x+18}&=&x\\ \sqrt[3]{x+3}&=&x-3\\ \sqrt{x+5}-\sqrt{x-3}&=&2 \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-08110299e31e4c6e2ed31acec0478893_l3.png)
Radical Equations may have one or more radical terms, and are solved by eliminating each radical, one at a time. We have to be careful when solving radical equations, as it is not unusual to find extraneous solutions. This is when we correctly solve an equation and one or more of the possible solutions are not correct due to taking both sides to a power and losing negative values. Therefore, it is imperative that solutions to radical equations always be checked in the original equation.
Radical Equations and How to Solve them
An equation containing terms with a variable in the radicand is called a radical equation.
To solve a radical equation:
- Isolate the radical expression on one side and put all remaining terms on the other side. (If there is more than one radical, just pick the hardest looking one first.)
- If the radical is a square root, then square both sides of the equation. If it is a cube root, cube both sides…if it is an nth root, take both sides to the nth power.
- Solve the remaining equation.
- If a radical term still remains, repeat steps 1-3.
- ALWAYS confirm solutions by substituting them into the original equation to look for extraneous solutions.
Example Solving an Equation with One Radical
Solve ![]()
Square both sides:
![]()
![]()
![]()
![]()
![]() or
or ![]()
Check our solutions:
-5: ![]()
![]()
![]() FALSE
FALSE
(Remember the square root symbol indicates the positive square root of a number, so -5 is NOT a solution to the equation, it is an extraneous solution)
3: ![]()
![]()
![]() TRUE
TRUE
So the solution to this equation is ![]() (
(![]() is extraneous)
is extraneous)
Try it Now 2
Solve the radical equation: ![]()
Hint: Remember that ![]()
Example Solving a Radical Equation Containing Two Radicals
Solve: ![]()
We need to pick one to isolate, so ![]() looks like the harder one, so lets subtract
looks like the harder one, so lets subtract ![]() from both sides:
from both sides:
![]()
Now square both sides:
![]()
![]()
We still have a radical, so we have to isolate that one now:
![]()
![]()
Square both sides again:
![]()
![]()
We can get rid of the fraction by multiplying both sides by 64:
![]()
Since this is quadratic, lets get everything on one side and 0 on the other and try to factor:
![]()
![]()
So ![]() or
or ![]()
Now we have to check our solutions in the original equations:
3: 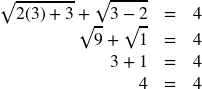
True, so ![]() is a solution to the equation.
is a solution to the equation.
83: 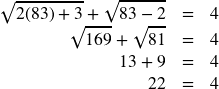
False, so ![]() is an extraneous solution.
is an extraneous solution.
The only solution is 3, with 83 being extraneous.
Try it Now 3
Solve the equations and check for extraneous solutions:
![]()
Try it Now Answers
- a.
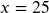 ; b.
; b. 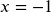
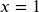 and
and 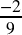 is extraneous
is extraneous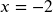 and -1 is extraneous
and -1 is extraneous
Media Attributions
- cuberootgraph
- sqrootgraph
- xto23power
- warningsign

