2.2 Domain and Range
One of our main goals in mathematics is to model the real world with mathematical functions. In doing so, it is important to keep in mind the limitations of those models we create.
This table shows a relationship between circumference and height of a tree as it grows.
| Circumference, c | 1.7 | 2.5 | 5.5 | 8.2 | 13.7 |
| Height, h | 24.5 | 31 | 45.2 | 54.6 | 92.1 |
While there is a strong relationship between the two, it would certainly be ridiculous to talk about a tree with a circumference of -3 feet, or a height of 3000 feet. When we identify limitations on the inputs and outputs of a function, we are determining the domain and range of the function.
Domain and Range
Domain: The set of possible input values to a function
Range: The set of possible output values of a function
Example of Domain and Range
- Using the tree table above, determine a reasonable domain and range.
We could combine the data provided with our own experiences and reason to approximate the domain and range of the function ![]() . For the domain, possible values for the input circumference
. For the domain, possible values for the input circumference ![]() , it doesn’t make sense to have negative values, so
, it doesn’t make sense to have negative values, so ![]() . We could make an educated guess at a maximum reasonable value, or look up that the maximum circumference measured is about 119 feet [1]. With this information we would say a reasonable domain is
. We could make an educated guess at a maximum reasonable value, or look up that the maximum circumference measured is about 119 feet [1]. With this information we would say a reasonable domain is ![]() feet.
feet.
Similarly for the range, it doesn’t make sense to have negative heights, and the maximum height of a tree could be looked up to be ![]() feet, so a reasonable range is
feet, so a reasonable range is ![]() feet.
feet.
2. When sending a letter through the United States Postal Service, the price depends upon the weight of the letter[2], as shown in the table below. Determine the domain and range.
| Weight Not Over (oz) | Price (Dollars) |
| 1 | 0.55 |
| 2 | 0.70 |
| 3 | 0.85 |
| 3.5 | 1.00 |
Since acceptable weights are 3.5 ounces or less, and negative weights don’t make sense, the domain would be ![]() . Suppose we notate Weight by
. Suppose we notate Weight by ![]() and Price by
and Price by ![]() , and set up a function named
, and set up a function named ![]() , where Price,
, where Price, ![]() is a function of Weight,
is a function of Weight, ![]() .
. ![]() .
.
Technically 0 could be included in the domain, but logically it would mean we are mailing nothing, so it doesn’t hurt to leave it out.
Since possible prices are from a limited set of values, we can only define the range of this function by listing the possible values. The range is p = {0.55, 0.70, 0.85, or 1.00}.
Try it Now 1
1. The population of a small town in the year 1960 was 100 people. Since then the population has grown to 1400 people reported during the 2010 census. Choose descriptive variables for your input and output and use interval notation to write the domain and range.
Interval Notation
In the previous examples, we used inequalities to describe the domain and range of the functions. This is one way to describe intervals of input and output values, but is not the only way. Let us take a moment to discuss notation for domain and range.
Using inequalities, such as ![]() ,
, ![]() , and
, and ![]() imply that we are interested in all values between the low and high values, including the high values in these examples.
imply that we are interested in all values between the low and high values, including the high values in these examples.
However, occasionally we are interested in a specific list of numbers like the range for the price to send letters. These numbers represent a set of specific values, so we encase them in curly brackets, {0.55, 0.70, 0.85, 1.00}.
Representing values as a set, or giving instructions on how a set is built, leads us to another type of notation to describe the domain and range.
Suppose we want to describe the values for a variable ![]() that are 10 or greater, but less than 30. In inequalities, we would write
that are 10 or greater, but less than 30. In inequalities, we would write ![]() .
.
A more compact alternative is interval notation, in which intervals of values are referred to by starting and ending values. Curved parentheses are used for “strictly less than,” and square brackets are used for “less than or equal to.” Since infinity is not a number, we can’t include it in the interval, so we always use curved parentheses with ![]() and
and ![]() .
.
The table below will help you see how inequalities correspond to interval notation:
| Inequality | Interval notation |
| all real numbers |
To combine two intervals together using inequalities, we can use the word “or”. In interval notation, we use the union symbol, ![]() to combine two unconnected intervals together.
to combine two unconnected intervals together.
Examples using Interval Notation
Describe the intervals of values shown on the line graph below using interval notations.
![]()
To describe the values, ![]() , that lie in the intervals shown above we would say, “
, that lie in the intervals shown above we would say, “![]() is a real number greater than or equal to 1 and less than or equal to 3, or a real number greater than 5.”
is a real number greater than or equal to 1 and less than or equal to 3, or a real number greater than 5.”
As an inequality it is: ![]() or
or ![]()
In interval notation: ![]()

Remember when writing or reading interval notation:
Using a square bracket [ means the start value is included in the set
Using a parenthesis ( means the start value is not included in the set
Try it Now 2
Describe the intervals of values shown on the line graph below using interval notation.
![]()
Domain and Range from Graphs
We can also talk about domain and range based on graphs. Since domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the graph. Remember that input values are almost always shown along the horizontal axis of the graph. Likewise, since range is the set of possible output values, the range of a graph we can see from the possible values along the vertical axis of the graph.
 Be careful – if the graph continues beyond the window on which we can see the graph, the domain and range might be larger than the values we can see.
Be careful – if the graph continues beyond the window on which we can see the graph, the domain and range might be larger than the values we can see.
Examples
Determine the domain and range of the graph below.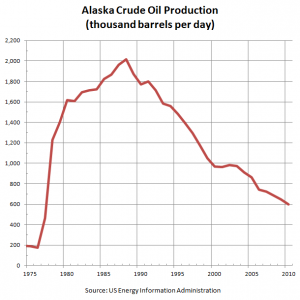 In the graph above, the input quantity along the horizontal axis appears to be “year”, which we could notate with the variable y. The output is “thousands of barrels of oil per day”, which we might notate with the variable,
In the graph above, the input quantity along the horizontal axis appears to be “year”, which we could notate with the variable y. The output is “thousands of barrels of oil per day”, which we might notate with the variable, ![]() for barrels. The graph would likely continue to the left and right beyond what is shown, but based on the portion of the graph that is shown to us, we can determine the domain is
for barrels. The graph would likely continue to the left and right beyond what is shown, but based on the portion of the graph that is shown to us, we can determine the domain is ![]() , and the range is approximately
, and the range is approximately ![]() .
.
In interval notation, the domain would be ![]() and the range would be about
and the range would be about ![]() . For the range, we have to approximate the smallest and largest outputs since they don’t fall exactly on the grid lines.
. For the range, we have to approximate the smallest and largest outputs since they don’t fall exactly on the grid lines.
 Remember that, as in the previous example, x and y are not always the input and output variables. Using descriptive variables is an important tool to remembering the context of the problem.
Remember that, as in the previous example, x and y are not always the input and output variables. Using descriptive variables is an important tool to remembering the context of the problem.
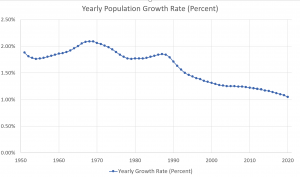
Try it Now 3
Given the graph below write the domain and range in interval notation.
Domain and Range from Formulas
So far we have examined domain and range in the context of data we are investigating. We also have domain and range restriction occurring from the function formula itself. In some cases, we may have two domain and ranges. One resulting from the formula and another in the context of the information. Most basic formulas can be evaluated at any input. However, two common restrictions are:
- The square root of negative values is non-real.
- We cannot divide by zero.
Examples Finding Domain and Range from Formulae
Find the domain of each function:
a. ![]()
Since we cannot take the square root of a negative number, we need the inside of the square root to be non-negative. So it must be true that:
![]() and solving this inequality by subtracting 4 from both sides means:
and solving this inequality by subtracting 4 from both sides means:
![]()
So the domain of ![]() .
.
b. ![]()
We cannot divide by zero, so we need the denominator to be non-zero.
Solving ![]()
![]()
![]()
so we must exclude 2 from the domain.
The domain of ![]() is
is ![]() .
.
Try it Now 4
Find the domain of each function:
a. ![]()
b. ![]()
Piecewise Functions
Some functions cannot be described by a single formula. So we have to define them in pieces with different formulas for different parts of the domain. Any ![]() values that are not specified would not be in the domain.
values that are not specified would not be in the domain.
Piecewise Functions
A piecewise function is a function in which the formula used depends upon the domain the input lies in. We notate this idea like:

Examples of Piecewise Functions
a. A museum charges $5 per person for a guided tour with a group of 1 to 9 people, or a fixed $50 fee for 10 or more people in the group. Set up a function relating the number of people, ![]() , to the cost,
, to the cost, ![]() .
.
Find the cost of using 1.5 gigabytes of data, and the cost of using 4 gigabytes of data.
To find the cost of using 1.5 gigabytes of data, ![]() , we first look to see which piece of the domain our input falls in. Since 1.5 is less than 2, we use the first formula, giving us
, we first look to see which piece of the domain our input falls in. Since 1.5 is less than 2, we use the first formula, giving us ![]() dollars.
dollars.
To find the cost of using 4 gigabytes of data, ![]() , we see that our input of 4 is greater than 2, so we’ll use the second formula:
, we see that our input of 4 is greater than 2, so we’ll use the second formula: ![]() dollars.
dollars.
c. Sketch a graph of the function 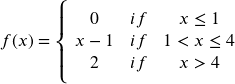
We can imagine graphing each function, then limiting the graph to the indicated domain. At the endpoints of the domain, we put open circles to indicate where the endpoint is not included, due to a strictly-less-than inequality, and a closed circle where the endpoint is included, due to a less-than-or-equal-to inequality. The first and last parts are constant functions, where the output is the same for all inputs. The middle part we might recognize as a line, and could graph by evaluating the function at a couple inputs and connecting the points with a line. Then, we combine them onto the same graph. When the first and second parts meet at ![]() , we can imagine the closed dot filling in the open dot. Since there is no break in the graph, there is no need to show the dot.
, we can imagine the closed dot filling in the open dot. Since there is no break in the graph, there is no need to show the dot.
Try in Now 5
At Pierce College during the 2009-2010 school year tuition rates for in-state residents were $89.50 per credit for the first 10 credits, $33 per credit for credits 11-18, and for over 18 credits the rate is 73 per credit[3]. Write a piecewise defined function for the total tuition, T, at Pierce College during 2009-2010 as a function of the number of credits taken, c. Be sure to consider a reasonable domain and range.
Try it Now Answers
- Domain; y = years [1960,2010] ; Range, p = population, [100,1400]
![Rendered by QuickLaTeX.com ( - \infty , - 2] \cup [ - 1,3)](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3942a93f69d1ab32c61d6a159e9ff012_l3.png)
- Domain: y = years [1951,2020]; Range: r = rate of population growth [1.05,2.09]
- a.
![Rendered by QuickLaTeX.com [3,\infty]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-3509e52e4e88823a79ca555e58979c23_l3.png) b.
b. ![Rendered by QuickLaTeX.com [-\infty, \frac{1}{2}] \cup [\frac{1}{2},\infty]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4ce64deb961ac49e55b24b379882d914_l3.png)
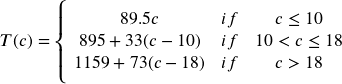
Tuition, ![]() , as a function of credits,
, as a function of credits, ![]() .
.
Reasonable domain should be whole numbers 0 to (answers may vary), e.g. [0,23]
Reasonable range should be 0 – (answers by vary), e.g. [0,1524]
Media Attributions
- Number line for Example
- Reminder is licensed under a Public Domain license
- Number Line for Try It Now
- warningsign
- Alaska_Crude_Oil_Production © RockyMtnGuy is licensed under a CC BY-SA (Attribution ShareAlike) license
- Worldpopulationgrowth

