5.2 Solving Quadratic Equations

As with any function, we can find the vertical intercepts of a quadratic by evaluating the function at an input of zero, and we can find the horizontal intercepts by solving for when the output will be zero.  Notice that depending upon the location of the graph, we might have zero, one, or two horizontal intercepts. However, before we get into these, we need to review complex numbers for those times when there are no real horizontal intercepts.

Review of Complex Numbers[1]

Recall that we usually restrict the domain of functions with square roots so that we do not have a negative value under the square root sign. This is because the square root of a negative number is not a real number. In other words, there is no way to square a real number and get a negative number. However, we have a way to denote the square root of -1 with an imaginary number, i.

Imaginary Numbers

The imaginary number, i is defined as i=\sqrt{-1} and any multiple of i is also an imaginary number.

Example of an Imaginary Number

Simplify \sqrt{-9}

We can separate \sqrt{-9} as \sqrt{9} \cdot \sqrt{-1}. We can take the square root of 9, and write the square root of -1 as i. 

\sqrt{-9}=\sqrt{9} \sqrt{-1} = 3i

A complex number is the sum of a real number and an imaginary number.

Complex Numbers

A complex number is a number z=a+bi, where a and b are real numbers

a  is the real part of the complex number

b  is the imaginary part of the complex number

i=\sqrt{-1}

For our purposes, we need to learn to simplify something like \dfrac{-4+\sqrt{-20}}{2}.  Simplifying means we write it in the form z=a+bi.

Example Writing a Complex Number in a+bi form.

Write \dfrac{-4+\sqrt{-20}}{2} in a+bi form.

The first thing we do is to think of this as \dfrac{1}{2} \left(-4+\sqrt{-20}\right)

Now distribute the \dfrac{1}{2}:   \dfrac{-4}{2}+\dfrac{\sqrt{-20}}{2}

The first fraction becomes -2 and the second we need to break up -20 into factors: -2+\dfrac{\sqrt{4} \sqrt{5} \sqrt{-1}}{2}

=-2+\dfrac{2\sqrt{5} \,\bf{i}}{2} = -2+ \sqrt{5}\,\bf{i}

Try it Now 1

Write \dfrac{-1+ \sqrt{-12}}{4} in a+bi form.

Intercepts of Quadratic Functions

Recall that depending on the location and direction of the parabola, quadratic functions can have 1, 2 or 0 real intercepts as illustrated below.

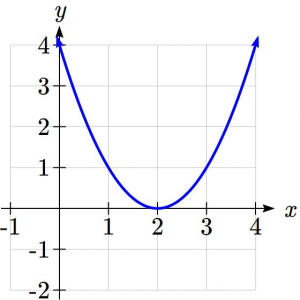
Illustration of parabola with one horizontal intercept
One Horizontal Intercept
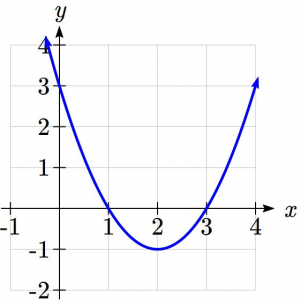
Illustration of two real intercepts
Two Real Horizontal Intercepts

 

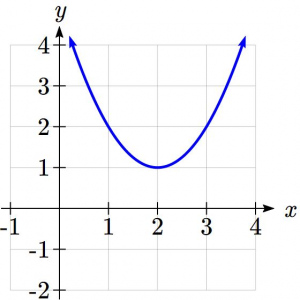
Illustration of zero real horizontal intercepts
Zero Real Horizontal Intercepts

In words, if we have two horizontal intercepts (also called x-intercepts or zeroes) the parabola dips down under the x-axis. If it is concave down, it would mean that the top is above the x-axis. For one horizontal intercepts, it means the turn-around point or vertex lies exactly on the x-axis. When there is zero real intercepts, it means that the parabola lies completely above the x-axis, if it is concave up or completely below, if it is concave down.

In order to find the horizontal intercepts, we need to know for what x-values is the function equal to zero.  In the case of quadratic functions, remember that we need to use one of the following methods.

Solving a Quadratic Equation by Factoring

To solve a factorable quadratic equation, ax^2+bx+c=0,we:

  1. Factor ax^2+bx+c=(dx+k)(px+q)
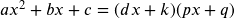
  2. Set each factor equal to 0 and solve:

dx+k = 0;\; x=\frac{-k}{d} or px+q=0;\;x=\frac{-q}{p}

Example Finding the Horizontal Intercepts

Find the vertical and horizontal intercepts of the quadratic f(x)=3x^2+5x-2.

We can find the vertical intercept by evaluating the function at an input of zero:
f(0)=3(0)^2+5(0)-2=-2 So the vertical intercept is at (0,-2).

For the horizontal intercepts, we solve for when output will be zero: 0=3x^2+5x-2

This can be factored easily so:
(3x-1)(x+2)=0
\begin{array}{lcr} 0=3x-1&\textsf{or}&0=x+2\\ x=\dfrac{1}{3}&\;&x=-2\end{array}
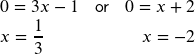
Horizontal intercepts at \left(\dfrac{1}{3},0 \right) and \left(-2,0 \right).

Try it Now 2

Find the vertical and horizontal intercepts of f(x)=5x^2+14x-3

Notice that in the standard form of a quadratic, the constant term c reveals the vertical intercept of the graph.

For quadratics that can’t be factored, we need another technique. Based on our previous work we showed that any quadratic in standard form can be written into vertex form as:

f(x) = a{\left( {x + \dfrac{b}{{2a}}} \right)^2} + c - \dfrac{{{b^2}}}{{4a}}

Solving for the horizontal intercepts using this general equation gives:
0 = a{\left( {x + \dfrac{b}{{2a}}} \right)^2} + c - \dfrac{{{b^2}}}{{4a}}

Start to solve for x by moving the constants to the other side:
\dfrac{{{b^2}}}{{4a}} - c = a{\left( {x + \dfrac{b}{{2a}}} \right)^2}

Divide both sides by a:
\dfrac{{{b^2}}}{{4{a^2}}} - \dfrac{c}{a} = {\left( {x + \dfrac{b}{{2a}}} \right)^2}

Find a common denominator to combine fractions:
\dfrac{{{b^2}}}{{4{a^2}}} - \dfrac{{4ac}}{{4{a^2}}} = {\left( {x + \dfrac{b}{{2a}}} \right)^2}

Combine the fractions on the left side of the equation:
\dfrac{{{b^2} - 4ac}}{{4{a^2}}} = {\left( {x + \dfrac{b}{{2a}}} \right)^2}

Take the square root of both sides:
\pm \sqrt {\dfrac{{{b^2} - 4ac}}{{4{a^2}}}} = x + \dfrac{b}{{2a}}

Subtract b/2a from both sides:
- \dfrac{b}{{2a}} \pm \dfrac{{\sqrt {{b^2} - 4ac} }}{{2a}} = x

Combining the fractions:
- \dfrac{b}{{2a}} \pm \dfrac{{\sqrt {{b^2} - 4ac} }}{{2a}} = x

Notice that this can yield two different answers for x:
x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}

Quadratic Formula

For a quadratic function given in standard form f(x)=ax^2+bx+c, the quadratic formula gives the horizontal intercepts of the graph of this function.

    \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\]

Examples Using Quadratic Formula

a. A ball is thrown upwards from the top of a 40 foot high building at a speed of 80 feet per second.  The ball’s height above ground can be modeled by the equation H(t)=-16t^2+80t+40. 
What is the maximum height of the ball?
When does the ball hit the ground?

To find the maximum height of the ball, we would need to know the vertex of the quadratic.
h = - \dfrac{{80}}{{2( - 16)}} = \dfrac{{80}}{{32}} = \dfrac{5}{2}
k = H\left( {\dfrac{5}{2}} \right) = - 16{\left( {\dfrac{5}{2}} \right)^2} + 80\left( {\dfrac{5}{2}} \right) + 40 = 140
The ball reaches a maximum height of 140 feet after 2.5 seconds.

To find when the ball hits the ground, we need to determine when the height is zero – when H(t) = 0. While we could do this using the transformation form of the quadratic, we can also use the quadratic formula:
t = \dfrac{{ - 80 \pm \sqrt {{{80}^2} - 4( - 16)(40)} }}{{2( - 16)}} = \dfrac{{ - 80 \pm \sqrt {8960} }}{{ - 32}}

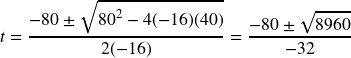
Since the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions:
t = \dfrac{{ - 80 - \sqrt {8960} }}{{ - 32}} \approx 5.458 or t = \dfrac{{ - 80 + \sqrt {8960} }}{{ - 32}} \approx - 0.458

The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds.

b. The supply for a certain product can be modeled by p=3q^2 and the demand can be modeled by p=1620-2q^2, where p is the price in dollars, and q is the quantity in thousands of items. Find the equilibrium price and quantity.

Recall that the equilibrium price and quantity is found by finding where the supply and demand curve intersect. We can find that by setting the equations equal:

\begin{array}{l} 3q^=1620-2q^2\\ 5q^2=1620\\ q^2=324\\ q=\pm \sqrt{324}=\pm 18 \end{array}

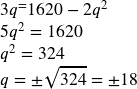
Since it doesn’t make sense to talk about negative quantities, the equilibrium quantity is q = 18.  To find the equilibrium price, we evaluate either function at the equilibrium quantity.
p=3(18)^2=972

The equilibrium is 18 thousand items, at a price of $972.

c. Find the horizontal intercepts of f(x) = -2x^2+5x-5

This does not seem easy to factor, so let’s use the quadratic formula:
a=-2, b=5, c=-5
\dfrac{-5 \pm \sqrt{5^2-4(-2)(-5)}}{2(-2)}=\dfrac{-5 \pm \sqrt{25-40}}{-4}=\dfrac{-5 \pm \sqrt{-15}}{-4}

We notice that this has a negative number under the radical, so the graph has no intercepts, but we want to give the complex roots of the quadratic in the form a+bi.
\dfrac{-5 \pm \sqrt{-15}}{-4}=\dfrac{-5}{-4} \pm \dfrac{\sqrt{-15}}{-4}=\dfrac{5}{4} \pm \dfrac{\sqrt{15}}{4}\,\bf{i}

Notice that I dropped the negative off the 4 in the denominator of the second term. This is because I’m adding or subtracting anyway so it doesn’t matter if it is positive or negative.

The two complex roots are: \dfrac{5}{4} + \dfrac{\sqrt{15}}{4}\,\bf{i} and \dfrac{5}{4} - \dfrac{\sqrt{15}}{4}\,\bf{i}

Try it Now 3

For these two equations, find the vertex, the vertical intercepts and horizontal intercepts, and tell if the vertex will be a maximum value or a minimum value.

a. g(x)=-8x+x^2+7

b. g(x)=-3(3-x)^2+2

Note that if the intercepts are real and easily graphed points, one can also use the vertex, intercepts and symmetry to graph a quadratic as well.

Try it Now Answers

  1. -\dfrac{1}{4}+\dfrac{\sqrt{3}}{2}\, \bf{i}
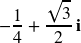
  2. Vertical Intercept: 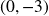(0,-3); Horizontal Intercepts: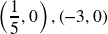\left(\dfrac{1}{5},0\right), \left(-3,0\right)
  3. a. Vertex at (4,-9) is a Minimum; Vertical Intercept at (0,7), Horizontal Intercepts at (7,0) and (1,0).   b.  Vertex at (3,2) is a Maximum; Vertical Intercept at (0, -25); Horizontal Intercepts at 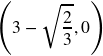\left(3-\sqrt{\dfrac{2}{3}},0 \right) and \left(3+\sqrt{\dfrac{2}{3}},0 \right)

 

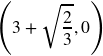
Media Attributions

  • onehorizint
  • twohorizint
  • zerohorizint
  1. This subsection is adapted from Precalculus: An Investigation of Functions (2nd Edition) by Lippman and Rasmussen licensed under a Creative Commons Attribution-Share Alike 3.0 United States License ↵

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

College Algebra for the Managerial Sciences Copyright © by Terri Manthey is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book