6.3 Proportion and Variation
A used-car company has just offered their best candidate, Uki, a position in sales. The position offers 16% commission on her sales. Her earnings depend on the amount of her sales. For instance, if she sells a vehicle for $4,600, she will earn $736. She wants to evaluate the offer, but she is not sure how. In this section, we will look at relationships like this one between earnings, sales and commission rate.
Solving Direct Variation Problems
In the example above, Uki’s earnings can be found by multiplying her sales by her commission. The formula ![]() tells us her earnings,
tells us her earnings, ![]() , are the product of 0.16, the commission rate and the sales price of the vehicle she sells,
, are the product of 0.16, the commission rate and the sales price of the vehicle she sells, ![]() . Consider if she sells a vehicle worth $9,200, she would then earn 0.16
. Consider if she sells a vehicle worth $9,200, she would then earn 0.16 ![]() $9,200 = $1,472 and an $18,400 vehicle would yield her $2,944 in earnings. Doubling the sales price of the vehicle also doubles her earnings. As the input increases, the output increases as a multiple of the input. A relationship in which one quantity is a constant multiplied by another quantity is called direct variation. Each variable in this type of relationship varies directly with the other.
$9,200 = $1,472 and an $18,400 vehicle would yield her $2,944 in earnings. Doubling the sales price of the vehicle also doubles her earnings. As the input increases, the output increases as a multiple of the input. A relationship in which one quantity is a constant multiplied by another quantity is called direct variation. Each variable in this type of relationship varies directly with the other.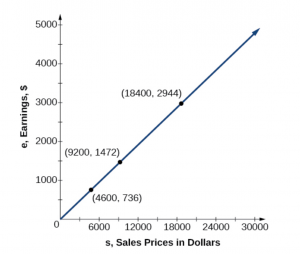
The graph shows the data for Uki’s potential earnings. We say that earnings vary directly with the sales price of the car. The general formula for direct variation is ![]() The value of
The value of ![]() is a constant greater than zero and is called the constant of variation. In this case,
is a constant greater than zero and is called the constant of variation. In this case, ![]() and
and ![]() . These are basically power functions.
. These are basically power functions.
Direct Variation
If ![]() and
and ![]() are related by an equation of the form:
are related by an equation of the form:
![]()
then we say that the relationship is direct variation and ![]() varies directly with, or is proportional to, the nth power of
varies directly with, or is proportional to, the nth power of ![]() . In direct variation relationships, there is a non-zero constant ratio
. In direct variation relationships, there is a non-zero constant ratio ![]() , where
, where ![]() is called the constant of variation, which help defines the relationship between the variables.
is called the constant of variation, which help defines the relationship between the variables.
Many times we are given a description of a direct variation problem and need to find an unknown. They key to these problems is to first find the constant of variation using what you know and then you are able to use your new formula to find the unknown quantity.
Example Solving a Direct Variation Problem
The quantity ![]() varies directly with the cube of
varies directly with the cube of ![]() . If
. If ![]() when
when ![]() , then find
, then find ![]() when
when ![]() is 6.
is 6.
First, we read the first sentence that ![]() varies directly with the cube of
varies directly with the cube of ![]() , this means
, this means ![]() and we have
and we have ![]() .
.
We can now use the ![]() and
and ![]() relationship given to find
relationship given to find ![]() :
:
![]()
![]()
So our direct variation formula becomes:
![]()
and we can plug in x:
![]()
We can see visual this with a graph as well: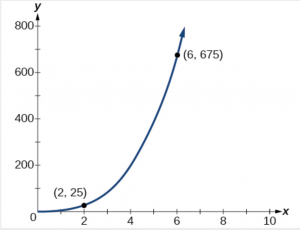
Note that our direct variation graphs look very different as the first one is linear and the previous example is cubic. These functions can be linear, quadratic, cubic, quartic or even radical, but they all pass through (0,0).
Try it Now 1
The quantity ![]() varies directly with the square of
varies directly with the square of ![]() . If
. If ![]() when
when ![]() , find
, find ![]() when
when ![]() is 4.
is 4.
Solving Inverse Variation Problems
The time is takes to double your money in an continuously compounded investment varies inversely to the interest rate. The formula ![]() gives us the approximate time it takes to double the money invested compounding continuously with interest rate,
gives us the approximate time it takes to double the money invested compounding continuously with interest rate, ![]() expressed as a decimal. If one invests in a continuously compounding account with an interest rate of 5% then it would take them 14 years to double their money. However, if the rate was 10%, they would double their money in only 7 years.
expressed as a decimal. If one invests in a continuously compounding account with an interest rate of 5% then it would take them 14 years to double their money. However, if the rate was 10%, they would double their money in only 7 years.
We notice in the relationship between these variables that, as one quantity was doubled, the other was cut in half. The two quantities are said to be inversely proportional and each term varies inversely with the other. Inversely proportion relationships are called inverse variations. See the graph below:
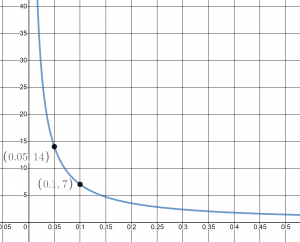
Inverse Variation
If ![]() and
and ![]() are related by an equation of the form:
are related by an equation of the form:
![]()
where ![]() is a nonzero constant, then we say that
is a nonzero constant, then we say that ![]() varies inversely with the nth power of
varies inversely with the nth power of ![]() . In inversely proportional relationships, or inverse variations, there is a constant multiply
. In inversely proportional relationships, or inverse variations, there is a constant multiply ![]()
Example Writing a Formula for an Inversely Proportional Relationship
A tourist plans to drive 100 miles. Find a formula for the time the trip will take as a function of the speed the tourist drives.
Recall that multiplying speed by time gives distance: ![]() . Because the distance is fixed at 100 miles, we have
. Because the distance is fixed at 100 miles, we have ![]() , so the time is takes will be given by
, so the time is takes will be given by ![]()
Time varies inversely with rate of speed.
Inverse variation problems are very similar to direct variation. We will first solve for ![]() using
using ![]() and then set up the formula and plug in the new
and then set up the formula and plug in the new ![]() to find the new
to find the new ![]() .
.
Example Solving an Inverse Variation Problem
A quantity ![]() varies inversely with the cube of
varies inversely with the cube of ![]() . If
. If ![]() when
when ![]() , find
, find ![]() when
when ![]() is 6.
is 6.
First we want to find k:
![]()
Now we have the formula:
![]()
And plug in the new ![]() :
:
![]()
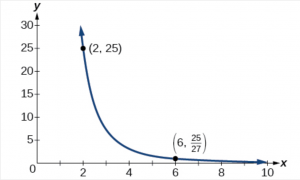
Try it Now 2
A quantity ![]() varies inversely with the square of
varies inversely with the square of ![]() . If
. If ![]() when
when ![]() , find
, find ![]() when
when ![]() is 4.
is 4.
Solving Problems Involving Joint Variation
Many situations are more complicated than a basic direct or inverse variation model. One variable often depends on multiple other variables. When a variable is dependent on the product or quotient of two or more variables, this is called joint variation. For example, the cost of busing students for each school trip varies with the number of students attending and the distance from the school. The variable ![]() , cost, varies jointly with the number of students,
, cost, varies jointly with the number of students, ![]() , and the distance,
, and the distance, ![]() .
.
Joint Variation
Joint variation occurs when a variable varies directly or inversely with multiple variables.
For instance, if ![]() varies directly with both
varies directly with both ![]() and
and ![]() , we have
, we have ![]() . If
. If ![]() varies directly with
varies directly with ![]() and inversely with
and inversely with ![]() we have
we have ![]() . Notice that we only use one constant in a joint variation equation.
. Notice that we only use one constant in a joint variation equation.
Example Solving a Problem Involving Joint Variation
A quantity ![]() varies directly with the square of
varies directly with the square of ![]() and inversely with the cube root of
and inversely with the cube root of ![]() . If
. If ![]() when
when ![]() and
and ![]() , find
, find ![]() when
when ![]() and
and ![]() .
.
We start with our general equation based on the description of the variation:
![Rendered by QuickLaTeX.com x=\dfrac{ky^2}{\sqrt[3]{z}}](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ab5ddf1c6b569b4bc3dbd62556f32591_l3.png)
Now we fill in what we know to find ![]() :
:
![Rendered by QuickLaTeX.com \begin{array}{l} 6=\dfrac{k(2)^2}{\sqrt[3]{8}}\\ 6=\dfrac{4k}{2}\\ 6=2k\\ k=3 \end{array}](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-36eed5c2dc568e2566fd7c7c26aac407_l3.png)
Now write our formula:
![Rendered by QuickLaTeX.com x=\dfrac{3y^2}{\sqrt[3]{z}}](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-28d2fc8a37227b2064882ebf66b7b867_l3.png)
And now plug in the new ![]() and
and ![]() :
:
![]()
Try it Now 3
A quantity ![]() varies directly with the square of
varies directly with the square of ![]() and inversely with
and inversely with ![]() . If
. If ![]() when
when ![]() and
and ![]() , find
, find ![]() when
when ![]() and
and ![]() .
.
Try it Now Answers
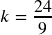 ;
; 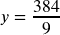
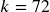 ;
; 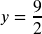
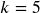 ;
; 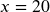
Media Attributions
- 63example1
- 63example2
- 63example3
- 63example4

