8.2 Annuites
For most of us, we aren’t able to put a large sum of money in the bank today. Instead, we save for the future by depositing a smaller amount of money from each paycheck into the bank. This idea is called a savings annuity. Most retirement plans like 401k plans or IRA plans are examples of savings annuities.
Suppose we will deposit $100 each month into an account paying 6% interest. How much will we have after a year? We assume that the account is compounded with the same frequency as we make deposits unless stated otherwise. In this example:
![]() or 6%
or 6%
![]() (12 compounds/deposits per year)
(12 compounds/deposits per year)
![]() (our deposit per month)
(our deposit per month)
![]() year
year
With ordinary annuities we assume the payment is made at the end of the period. The $100 we deposit at the end of the first month will earn interest for 11 months and at the end of the year will be worth ![]()
The $100 deposited at the end of the second month will have 10 months to grow, and will be worth ![]() at the end of the year. This pattern continues down to the last deposit, which has no time to compound, and will be worth
at the end of the year. This pattern continues down to the last deposit, which has no time to compound, and will be worth ![]() .
.
In total, we will have accumulated:
![]()
This equation leaves a lot to be desired, though – it doesn’t make calculating the ending balance any easier! To simplify things, multiply both sides of the equation by 1.005:
![]()
Distributing on the right side of the equation gives:
![]()
Now we’ll line this up with like terms from our original equation, and subtract each side:
![]()
Almost all the terms cancel on the right-hand side when we subtract, leaving:
![]()
Now we can solve this equation for ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{array}{l} 0.005A = 100\left( {{{\left( {1.005} \right)}^{12}} - 1} \right)\\ \;\\ A = \dfrac{{100\left( {{{\left( {1.005} \right)}^{12}} - 1} \right)}}{{0.005}} \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-70fea0f31f1450f0b07dc806ce5a3cd1_l3.png)
Recall 0.005 was r/k, 100 was the deposit d, and 12 was the number of months, kt. Generalizing this result, we get the saving annuity formula.
Annuity Formula
![Rendered by QuickLaTeX.com \[A = \dfrac{{d\left( {{{\left( {1 + \dfrac{r}{k}} \right)}^{kt}} - 1} \right)}}{{\left( {\dfrac{r}{k}} \right)}}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-68c32d5b55051c81fa04d06ef6557edc_l3.png)
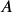 is the balance in the account after
is the balance in the account after 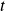 years.
years.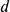 is the regular deposit (the amount you deposit each year, each month, etc.)
is the regular deposit (the amount you deposit each year, each month, etc.) is the annual interest rate in decimal form.
is the annual interest rate in decimal form.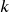 is the number of compounding periods in one year.
is the number of compounding periods in one year.
If the compounding frequency is not explicitly stated, assume there are the same number of compounds in a year as there are deposits made in a year.
For example, if the compounding frequency isn’t stated:
- If you make your deposits every month, use monthly compounding,
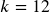 .
. - If you make your deposits every year, use yearly compounding,
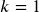 .
. - If you make your deposits every quarter, use quarterly compounding,
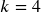 .
.
Etc.
Annuities assume that you put money in the account on a regular schedule (every month, year, quarter, etc.) and let it sit there earning interest.
Compound interest assumes that you put money in the account once and let it sit there earning interest.
Compound interest: One deposit
Annuity: Many deposits
Example of an Annuity
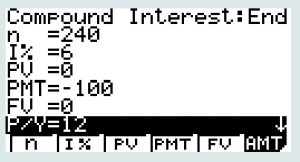
A traditional individual retirement account (IRA) is a special type of retirement account in which the money you invest is exempt from income taxes until you withdraw it. If you deposit $100 each month into an IRA earning 6% interest, how much will you have in the account after 20 years?
In this example,
![]() the monthly deposit
the monthly deposit
![]() 6% annual rate
6% annual rate
![]() since we’re doing monthly deposits, we’ll compound monthly
since we’re doing monthly deposits, we’ll compound monthly
![]() we want the amount after 20 years
we want the amount after 20 years
Putting this into the equation:
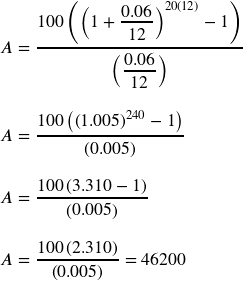
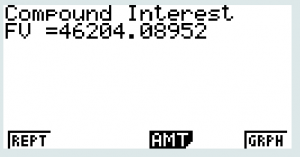
The account will grow to $46,200 after 20 years.
Notice that you deposited into the account a total of $24,000 ($100 a month for 240 months). The difference between what you end up with and how much you put in is the interest earned. In this case it is $46,200 – $24,000 = $22,200.
Using Technology
Similar to the compound interest in the last section, we can use TVM Solver on a calculator or Excel to solve these problems as well.
On a TI 83/84 Calculator
Once again, we go to APPS and 1: Finance and 1: TVM Solver. The difference now is that our PV, or present value is 0 as we are starting with nothing, and we enter the negative of the deposit in for PMT (payment) because we are taking that money away from us into the account. We put the cursor on which we want to solve and hit ALPHA-ENTER.
For the previous example:
| Enter the Information | After going to FV and ALPHA-ENTER |
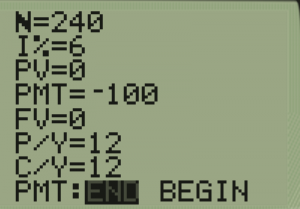 |
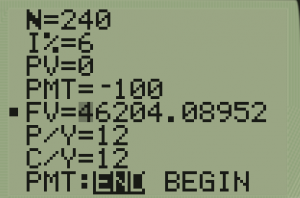 |
Notice that our final amount we have in the account here is a little larger than the answer we got by hand. This was intermediate round-off error on ![]() . Our answer in TVM solver is actually more accurate.
. Our answer in TVM solver is actually more accurate.
On CASIO
Again, this is similar to our procedure in the last section. Go to Menu-TVM and F2: for Compound Interest as it will allow us to put a PMT there. We fill in everything as before except we start with 0, so our PV or present value is 0 and PMT is negative of the deposit amount.
For the previous example:
| Enter the Information: | After hitting F5 to find FV: |
 |
 |
In Excel or Google Sheets
In Excel or Google Sheets, there are several commands that figure compound interest for annuities:
- =FV(r/k, kt, -d, 0) will provide the A or future value, given the other variables (Note: put the deposit in as a negative value)
- =PMT(r/k, kt, 0, A) will provide the -deposit or the negative of the payment needed to have a given amount of money in the account after t years.
- =NPER(r/k, -d, 0, A) will give the number of periods necessary to have the amount needed. This can be divided by k to find the number of years.
- =RATE(kt, -d, 0, A) will give the rate necessary to make A out of P in t years compounding k times a year.
For our previous example, we would type in =FV(0.005, 240, -100,0)
Example Finding Deposit Needed to Reach a Goal
You want to have $200,000 in your account when you retire in 30 years. Your retirement account earns 8% interest. How much do you need to deposit each month to meet your retirement goal?
In this example,
We’re looking for ![]() .
.
![]() or 8% annual rate
or 8% annual rate
![]() since we’re depositing monthly
since we’re depositing monthly
![]() years
years
![]() The amount we want to have in 30 years
The amount we want to have in 30 years
In this case, we’re going to have to set up the equation, and solve for ![]() .
.
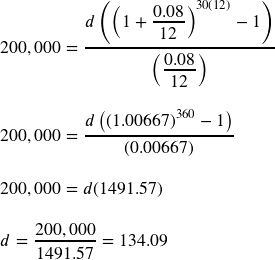
So you would need to deposit $134.09 each month to have $200,000 in 30 years if your account earns 8% interest.
Alternatively, you could use a calculator or Excel. On Calculator, the TVM solver would be filled in as:
N = 360
I% = 6
PV = 0
PMT = 0 for now – or it doesn’t matter as this is what we are solving for)
FV = 200000
P/Y = 12
C/Y = 12
END
On a TI: Cursor back to PMT and hit ALPHA-ENTER and PMT will change to -134.1958… or in this case our deposit should really be $134.20.
On the CASIO: Hit F4 for PMT and it calculates the same as the TI.
On Excel: =PMT(.08/12, 360, 0, 200000)
Note in Excel, we put .08/12 to keep the exact value instead of the round-off to avoid errors.
Try it Now
A more conservative investment account pays 3% interest. If you deposit $5 a day into this account, how much will you have after 10 years? How much is from interest?
Example of Determining How Long an Annuity will Require
If you invest $100 each month into an account earning 3% compounded monthly, how long will it take the account to grow to $10,000?
This is a savings annuity problem since we are making regular deposits into the account.
![]() the monthly deposit
the monthly deposit
![]() or 3% annual rate
or 3% annual rate
![]() since we’re doing monthly deposits, we’ll compound monthly
since we’re doing monthly deposits, we’ll compound monthly
We don’t know ![]() , but we want
, but we want ![]() to be $10,000.
to be $10,000.
Putting this into the equation:
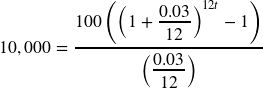
![]()
We want to isolate the exponential term, ![]() , so multiply both sides by 0.0025
, so multiply both sides by 0.0025
![]()
![]()
![]()
![]()
![]()
![]()
![]() years
years
It will take about 7.447 years to grow the account to $10,000.
Alternatively, you could use a calculator or Excel. On Calculator, the TVM solver would be filled in as:
N = 0 for now, or again, it does not matter as we are going to solve it
I% = 3
PV = 0
PMT =-100
FV = 10000
P/Y = 12
C/Y = 12
END
On a TI: Cursor back to N and hit ALPHA-ENTER and N will change to 89.3689…. This is the number of months. We need to use 2nd MODE (Quit) to leave this screen and go to the main screen and find 89.3689/12 = 7.447 years
On the CASIO: Hit F4 for N and it calculates the same as the TI. You can exit and divide by 12.
On Excel: =NPER(.03/12, -100, 0, 10000) and on the next line, it is easy to hit = A1/12 (assuming A1 is where the NPER command was, it’s the cell designation).
Try it Now Answer
![]() the daily deposit
the daily deposit
![]() 3% annual rate
3% annual rate
![]() since we’re doing daily deposits, we’ll compound daily
since we’re doing daily deposits, we’ll compound daily
![]() we want the amount after 10 years
we want the amount after 10 years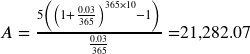
We would have deposited a total of $5·365·10 = $18,250, so $3,032.07 is from interest.
Media Attributions
- 82example1
- 82example2
- 82example3
- 82example4

