7.3 Exponential and Logarithmic Models

While we have explored some basic applications of exponential and logarithmic functions, in this section we explore some important applications in more depth.

More complex exponential equations can often be solved in more than one way.  In the following example, we will solve the same problem in two ways – one using logarithm properties, and the other using exponential properties.

Application Example Log first Method

In 2008, the population of Kenya was approximately 38.8 million, and was growing by 2.64% each year, while the population of Sudan was approximately 41.3 million and growing by 2.24% each year[1].  If these trends continue, when will the population of Kenya match that of Sudan?

We start by writing an equation for each population in terms of t, the number of years after 2008.
\begin{array}{l} Kenya(t) = 38.8{(1 + 0.0264)^t}\\ Sudan(t) = 41.3{(1 + 0.0224)^t} \end{array}

To find when the populations will be equal, we can set the equations equal:
38.8{(1.0264)^t} = 41.3{(1.0224)^t}

For our first approach, we take the log of both sides of the equation:
\log\left( {38.8{{(1.0264)}^t}} \right) = \log\left( {41.3{{(1.0224)}^t}} \right)

Utilizing the sum property of logs, we can rewrite each side,
\log(38.8) + \log\left( {{{1.0264}^t}} \right) = \log(41.3) + \log\left( {{{1.0224}^t}} \right)

Then utilizing the exponent property, we can pull the variables out of the exponent:
\log(38.8) + t\log\left( {1.0264} \right) = \log(41.3) + t\log\left( {1.0224} \right)

Moving all the terms involving t to one side of the equation and the rest of the terms to the other side,
t\log\left( {1.0264} \right) - t\log\left( {1.0224} \right) = \log(41.3) - \log(38.8)

Factoring out the t on the left,
t\left( {\log\left( {1.0264} \right) - \log\left( {1.0224} \right)} \right) = \log(41.3) - \log(38.8)

Dividing to solve for t
t = \dfrac{{\log(41.3) - \log(38.8)}}{{\log\left( {1.0264} \right) - \log\left( {1.0224} \right)}} \approx 15.991 years until the populations will be equal.

Same Example Using Exponentials First

Solve the problem above by rewriting before taking the log.

Starting at the equation:
38.8{(1.0264)^t} = 41.3{(1.0224)^t}

Divide to move the exponential terms to one side of the equation and the constants to the other side:
\dfrac{{{{1.0264}^t}}}{{{{1.0224}^t}}} = \dfrac{{41.3}}{{38.8}}

Using exponent rules to group on the left,
{\left( {\dfrac{{1.0264}}{{1.0224}}} \right)^t} = \dfrac{{41.3}}{{38.8}}

Taking the log of both sides:
\log\left( {{{\left( {\dfrac{{1.0264}}{{1.0224}}} \right)}^t}} \right) = \log\left( {\dfrac{{41.3}}{{38.8}}} \right)

Utilizing the exponent property on the left,
t\log\left( {\dfrac{{1.0264}}{{1.0224}}} \right) = \log\left( {\dfrac{{41.3}}{{38.8}}} \right)

Dividing gives:
t = \dfrac{{\log\left( {\dfrac{{41.3}}{{38.8}}} \right)}}{{\log\left( {\dfrac{{1.0264}}{{1.0224}}} \right)}} \approx 15.991 years.

While the answer does not immediately appear identical to that produced using the previous method, note that by using the difference property of logs, the answer could be rewritten:
t = \dfrac{\log\left( \dfrac{41.3}{38.8} \right)}{\log\left( \dfrac{1.0264}{1.0224} \right)} = \dfrac{\log(41.3) - \log(38.8)}{\log(1.0264) - \log(1.0224)}

While both methods work equally well, it often requires fewer steps to utilize algebra before taking logs, rather than relying solely on log properties.

Try it Now 1

Tank A contains 10 liters of water, and 35% of the water evaporates each week.  Tank B contains 30 liters of water, and 50% of the water evaporates each week.  In how many weeks will the tanks contain the same amount of water?

Radioactive Decay

In an earlier section, we discussed radioactive decay – the idea that radioactive isotopes change over time.  One of the common terms associated with radioactive decay is half-life.

Half Life

The half-life of a radioactive isotope is the time it takes for half the substance to decay.

Given the basic exponential growth/decay equation h(t)=ab^t, half-life can be found by solving for when half the original amount remains; by solving \dfrac{1}{2}a=a(b)^t, or more simply \dfrac{1}{2}=b^t.  Notice how the initial amount is irrelevant when solving for half-life.

Example finding half-life

Bismuth-210 is an isotope that decays by about 13% each day.  What is the half-life of Bismuth-210?

We were not given a starting quantity, so we could either make up a value or use an unknown constant to represent the starting amount. To show that starting quantity does not affect the result, let us denote the initial quantity by the constant a. Then the decay of Bismuth-210 can be described by the equation Q(d) = a{(0.87)^d}.

To find the half-life, we want to determine when the remaining quantity is half the original: \frac{1}{2}a . Solving,

\dfrac{1}{2}a = a{(0.87)^d}

Dividing by a:
\dfrac{1}{2} = {0.87^d}

Take the log of both sides:
\log \left( {\dfrac{1}{2}} \right) = \log \left( {{{0.87}^d}} \right)

Use the exponent property of logs:
\log \left( {\dfrac{1}{2}} \right) = d\log \left( {0.87} \right)

Divide to solve for d:
d = \dfrac{{\log\left( {\dfrac{1}{2}} \right)}}{{\log\left( {0.87} \right)}} \approx 4.977 days

This tells us that the half-life of Bismuth-210 is approximately 5 days.

Example using Half-life

Cesium-137 has a half-life of about 30 years.  If you begin with 200mg of cesium-137, how much will remain after 30 years?  60 years?  90 years?

Since the half-life is 30 years, after 30 years, half the original amount, 100mg, will remain.

After 60 years, another 30 years have passed, so during that second 30 years, another half of the substance will decay, leaving 50mg.

After 90 years, another 30 years have passed, so another half of the substance will decay, leaving 25mg.

Example of Carbon Dating

Carbon-14 is a radioactive isotope that is present in organic materials, and is commonly used for dating historical artifacts.   Carbon-14 has a half-life of 5730 years.  If a bone fragment is found that contains 20% of its original carbon-14, how old is the bone?

To find how old the bone is, we first will need to find an equation for the decay of the carbon-14.  We could either use a continuous or annual decay formula, but opt to use the continuous decay formula since it is more common in scientific texts.  The half life tells us that after 5730 years, half the original substance remains.  Solving for the rate,
\dfrac{1}{2}a = a{e^{r5730}}

Divide by a:
\dfrac{1}{2} = {e^{r5730}}

Take natural log of both sides:
\ln \left( {\dfrac{1}{2}} \right) = \ln \left( {{e^{r5730}}} \right)

Use inverse property of logs on the right:
\ln \left( {\dfrac{1}{2}} \right) = 5730r

Divide by 5730:
r = \dfrac{{\ln \left( {\dfrac{1}{2}} \right)}}{{5730}} \approx - 0.000121

Now we know the decay will follow the equation Q(t) = a{e^{ - 0.000121t}}. To find how old the bone fragment is that contains 20% of the original amount, we solve for t so that Q(t)=0.20a

0.20a = a{e^{ - 0.000121t}}

0.20 = {e^{ - 0.000121t}}

\ln (0.20) = \ln \left( {{e^{ - 0.000121t}}} \right)

\ln (0.20) = - 0.000121t

t = \dfrac{{\ln (0.20)}}{{ - 0.000121}} \approx 13301 years

The bone fragment is about 13,300 years old.

Try it Now 2

In Example 3, we learned that Cesium-137 has a half-life of about 30 years.  If you begin with 200mg of cesium-137, how long will it take until only 1 milligram remains?

For decaying quantities, we asked how long it takes for half the substance to decay.  For growing quantities we might ask how long it takes for the quantity to double.

Doubling Time

The doubling time of a growing quantity is the time it takes for the quantity to double.

Given the basic exponential growth equation h(t)=ab^t, doubling time can be found by solving for when the original quantity has doubled; by solving 2a=ab^x, or more simply 2=b^x.  Again notice how the initial amount is irrelevant when solving for doubling time.

Example Doubling Time

If you invest money at 8% compounded quarterly, how long will it take your money to double?

Using the compound interest equation, we can write A(t) = P{\left( {1 + \dfrac{{0.08}}{4}} \right)^{4t}} = P{(1.02)^{4t}}.

To find the doubling time, we look for the time until we have twice the original amount, so when A(t) = 2P. Notice we don’t need to know how much was invested.

2P = P{(1.02)^{4t}}
2 = {(1.02)^{4t}}
\ln \left( 2 \right) = \ln \left( {{{1.02}^{4t}}} \right)
\ln \left( 2 \right) = 4t\ln \left( {1.02} \right)
t = \dfrac{{\ln \left( 2 \right)}}{{4\ln \left( {1.02} \right)}} \approx 8.751

It will take about 8.75 years for the investment to double.

Example Using doubling time for Predictions

Use of a new social networking website has been growing exponentially, with the number of new members doubling every 5 months.  If the site currently has 120,000 users and this trend continues, how many users will the site have in 1 year?

We can use the doubling time to find a function that models the number of site users, and then use that equation to answer the question. While we could use an arbitrary a as we have before for the initial amount, in this case, we know the initial amount was 120,000.

If we use a continuous growth equation, it would look like N(t) = 120{e^{rt}}, measured in thousands of users after t months. Based on the doubling time, there would be 240 thousand users after 5 months. This allows us to solve for the continuous growth rate:
240 = 120{e^{r5}}
2 = {e^{r5}}
\ln 2 = 5r

r = \dfrac{{\ln 2}}{5} \approx 0.1386

Now that we have an equation, N(t) = 120{e^{0.1386t}}, we can predict the number of users after 12 months:
N(12) = 120{e^{0.1386(12)}} = 633.140 thousand users

So after 1 year, we would expect the site to have around 633,140 users.

Try it Now 3

If tuition at a college is increasing by 6.6% each year, how many years will it take for tuition to double?

Logarithmic Scales

For quantities that vary greatly in magnitude, a standard linear scale of measurement is not always effective, and utilizing logarithms can make the values more manageable.  For example, if the average distances from the sun to the major bodies in our solar system are listed, you see they vary greatly.

Planet Distance (millions of km)
Mercury 58
Venus 108
Earth 150
Mars 228
Jupiter 779
Saturn 1430
Uranus 2880
Neptune 4500

Placed on a linear scale – one with equally spaced values – these values get bunched up.

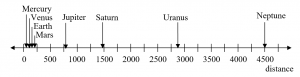
Line showing distance from sun of planets on linear scale

However, computing the logarithm of each value and plotting these new values on a number line results in a more manageable graph, and makes the relative distances more apparent.

Planet Distance (millions of km) log(distance)
Mercury 58 1.76
Venus 108 2.03
Earth 150 2.18
Mars 228 2.36
Jupiter 779 2.89
Saturn 1430 3.16
Uranus 2880 3.46
Neptune 4500 3.65

Showing Distance Sun to Planets on Logarithmic Scale

Sometimes, as shown above, the scale on a logarithmic number line will show the log values, but more commonly the original values are listed as powers of 10, as shown below.

Line showing how logarithmic scales are often labeled

Example Estimating Values from a Logarithmic Scale

Estimate the value of point P on the log scale above

The point P appears to be half way between -2 and -1 in log value, so if V is the value of this point,
\log (V) \approx - 1.5

Rewriting in exponential form:
V \approx {10^{ - 1.5}} = 0.0316

Example Placing a Number on a Logarithmic Scale

Place the number 6000 on a logarithmic scale.

Since \log (6000) \approx 3.8, this point would belong on the log scale about here:

Log scale showing 6000

Try it Now 4

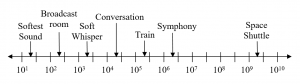
Plot the data in the table below on a logarithmic scale.[2]

Source of Sound/Noise Approximate Sound Pressure
in µPa (micro Pascals)
Launching of the Space Shuttle 2,000,000,000
Full Symphony Orchestra 2,000,000
Diesel Freight Train at High Speed at 25 m 200,000
Normal Conversation 20,000
Soft Whispering at 2 m in Library 2,000
Unoccupied Broadcast Studio 200
Softest Sound a human can hear 20

It is also common to see two dimensional graphs with one or both axes using a logarithmic scale.  One common use of a logarithmic scale on the vertical axis is to graph quantities that are changing exponentially, since it helps reveal relative differences.  This is commonly used in stock charts, since values historically have grown exponentially over time.   Both stock charts below show the Dow Jones Industrial Average, from 1915 to 2020.

 

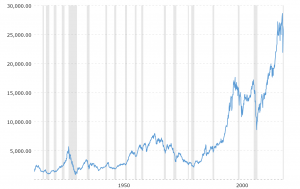
100 year Dow Jones Average on Linear Scale
Dow Jones Industrial average on Linear Scale

 

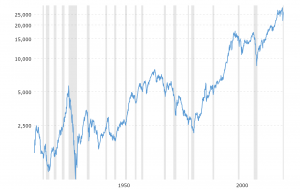
Dow Jones 100 Year average on Log Scale
Dow Jones 100-year Industrial Average on Logarithmic Scale

Both charts have a linear horizontal scale, but the first graph has a linear vertical scale, while the second has a logarithmic vertical scale.  The first scale is the one we are more familiar with, and shows what appears to be a strong exponential trend.

Example of Assessing Stock Market Changes

There were stock market drops in 1929, 2008 and 2020.  Which was largest?  Which was smallest?

In the first graph, the stock market drop around 2008 and again in 2020 both look very large, and in terms of dollar values, they were indeed large drops. In 2008, it went from about 16500 to 8500 fairly quickly.  A difference of 8000.  In 2020, it went from 28500 to 2200, a difference of 6000.  However the second graph shows relative changes, and the drop in 2008 seems less major on this graph, and in fact the drop starting in 1929 was, percentage-wise, much more significant.

In 2008,  percentage-wise, there was a 48% drop and in 2020, at 21% drop. In 1929, the Dow value dropped from 5500 to 812 in June of 1932. While value-wise this drop of 4688 is smaller than the 2008 drop, it corresponds to a 85% drop, a much larger relative drop than in 2008. The logarithmic scale shows these relative changes.

Try it Now Answers

  1. 4.1874 weeks
  2. 229.3157 or approximately 229 years
  3. It will take 10.845 years, or approximately 11 years, for tuition to double.
  4. Try it Now 4 Answer

Media Attributions

  1. World Bank, World Development Indicators, as reported on http://www.google.com/publicdata, retrieved August 24, 2010 ↵
  2. From http://www.epd.gov.hk/epd/noise_education/web/ENG_EPD_HTML/m1/intro_5.html, retrieved Oct 2, 2010 ↵

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

College Algebra for the Managerial Sciences Copyright © by Terri Manthey is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book