6.7 Transformation of Functions
Often when given a problem, we try to model the scenario using mathematics in the form of words, tables, graphs and equations in order to explain or solve it. When building models, it is often helpful to build off of existing formulas or models. Knowing the basic graphs of your tool-kit functions can help you solve problems by being able to model new behavior by adapting something you already know. Unfortunately, the models and existing formulas we know are not always exactly the same as the ones presented in the problems we face.
Fortunately, there are systematic ways to shift, stretch, compress, flip and combine functions to help them become better models for the problems we are trying to solve. We can transform what we already know into what we need, hence the name, “Transformation of functions.” When we have a story problem, formula, graph, or table, we can then transform that function in a variety of ways to form new functions.
Parent Functions
Before we begin transforming them, let’s review the parent functions that everyone should know.
| Function | Graph | Domain | Range |
| Linear |
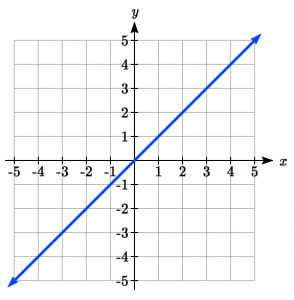 |
||
| Absolute Value: |
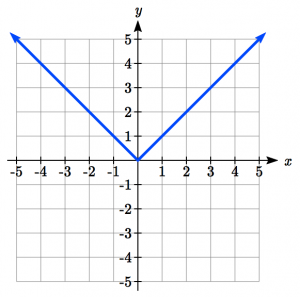 |
||
| Quadratic: |
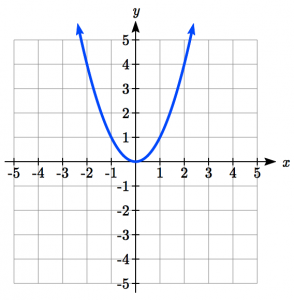 |
||
| Cubic: |
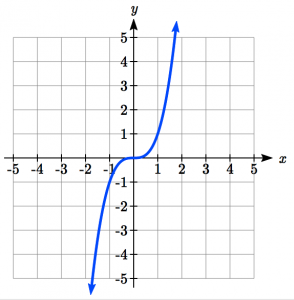 |
||
| Square Root: |
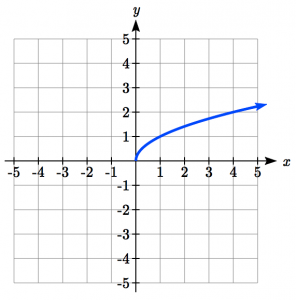 |
||
| Cube Root: |
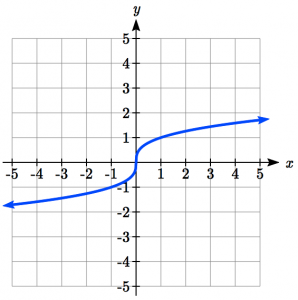 |
||
| Reciprocal: |
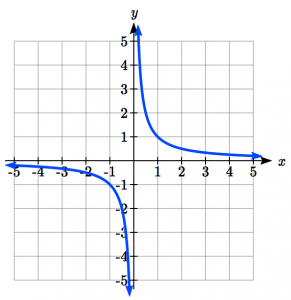 |
||
| Reciprocal Squared: |
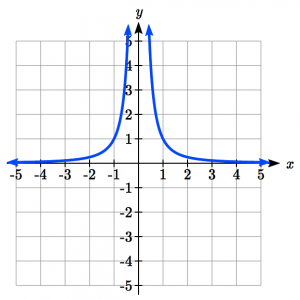 |
Knowing these functions, we can consider how to transform them, which creates a much easier way to graph, or sketch many different functions.
Shifts
If we want to look at the function ![]() , we know from graphing quadratic functions that this means the vertex is (0,4) instead of (0,0) which is the vertex of the parent function,
, we know from graphing quadratic functions that this means the vertex is (0,4) instead of (0,0) which is the vertex of the parent function, ![]() . Notice that this moves up the vertex 4 units.
. Notice that this moves up the vertex 4 units. 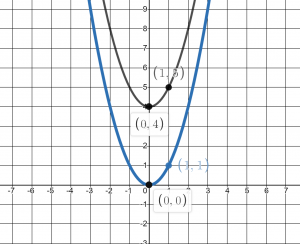
Similarly, we could look at the other points, such as ![]() and
and ![]() , which are 1 and 5 respectively, we see that
, which are 1 and 5 respectively, we see that ![]() is just the graph
is just the graph ![]() moved up 4 units.
moved up 4 units.
This is an example of a vertical shift. The input values stay the same and only the output values change. The range also changes. The range of ![]() is
is ![]() and the range of
and the range of ![]() is moved up 4 with the graph to
is moved up 4 with the graph to ![]()
Vertical Shift
Given a function ![]() , if we define a new function
, if we define a new function ![]() as
as
![]() , where
, where ![]() is a constant
is a constant
then ![]() is a vertical shift of the function
is a vertical shift of the function ![]() , where all the output values have been increased by
, where all the output values have been increased by ![]() .
.
If ![]() is positive, then the graph will shift up
is positive, then the graph will shift up
If ![]() is negative, then the graph will shift down
is negative, then the graph will shift down
Example of a Vertical Shift with a Function Defined as a Table
A function ![]() is given as a table below. Create a table for the function
is given as a table below. Create a table for the function ![]()
| x | 2 | 4 | 6 | 8 |
| f(x) | 1 | 3 | 7 | 11 |
The formula ![]() tells us that we can find the output values of the g function by subtracting 3 from the output values of the f function. For example,
tells us that we can find the output values of the g function by subtracting 3 from the output values of the f function. For example,
![]()
![]()
![]()
Subtracting 3 from each ![]() value, we can complete a table of values for
value, we can complete a table of values for ![]()
| x | 2 | 4 | 6 | 8 |
| g(x) | -2 | 0 | 4 | 8 |
As with the earlier vertical shift, notice the input values stay the same and only the output values change.
Try it Now 1
The function ![]() gives the height h of a ball (in meters) thrown upwards from the ground after t seconds. Suppose the ball was instead thrown from the top of a 10 meter building. Relate this new height function b(t) to h(t), then find a formula for b(t).
gives the height h of a ball (in meters) thrown upwards from the ground after t seconds. Suppose the ball was instead thrown from the top of a 10 meter building. Relate this new height function b(t) to h(t), then find a formula for b(t).
The vertical shift is a change to the output, or outside, of the function. We will now look at how changes to input, on the inside of the function, change its graph and meaning.
Consider the function ![]() . In a similar, parent function,
. In a similar, parent function, ![]() , there is a point in the center at (0,0). But, in order for
, there is a point in the center at (0,0). But, in order for ![]() to have an output of 0,
to have an output of 0, ![]() would have to be
would have to be ![]() . So we have a point at (4,0). Now consider, what we would need to have an output of 1.
. So we have a point at (4,0). Now consider, what we would need to have an output of 1.
![]()
Take the cube root of both sides:
![]()
![]()
![]()
So we have a point at (5,1) for ![]() and (1,1) for
and (1,1) for ![]() Notice that now the outputs stay the same, but the inputs change.
Notice that now the outputs stay the same, but the inputs change. ![]() is
is ![]() moved to the right 4 units as seen below:
moved to the right 4 units as seen below:
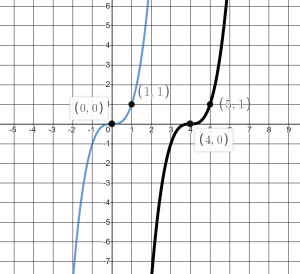
Horizontal changes or “inside changes” affect the domain of a function (the input) instead of the range and often seem counter-intuitive. The new function ![]() uses the same outputs as
uses the same outputs as ![]() , but matches those outputs to inputs 4 units less than those of
, but matches those outputs to inputs 4 units less than those of ![]() . Said another way, we must add 4 to the input of
. Said another way, we must add 4 to the input of ![]() to find the corresponding output for
to find the corresponding output for ![]() :
: ![]() .
.
Horizontal Shift
Given a function ![]() , if we define a new function
, if we define a new function ![]() as
as
![]() , where
, where ![]() is a constant
is a constant
then ![]() is a horizontal shift of the function
is a horizontal shift of the function ![]()
If h is positive, then the graph will shift right
If h is negative, then the graph will shift left
Example of a Horizontal Shift with a Table
A function ![]() is given as a table below. Create a table for the function
is given as a table below. Create a table for the function ![]()
| x | 2 | 4 | 6 | 8 |
| f(x) | 1 | 3 | 7 | 11 |
The formula ![]() tells us that the output values of g are the same as the output value of f with an input value three smaller. For example, we know that . To get the same output from the g function, we will need an input value that is 3 larger: We input a value that is three larger for g(x) because the function takes three away before evaluating the function f.
tells us that the output values of g are the same as the output value of f with an input value three smaller. For example, we know that . To get the same output from the g function, we will need an input value that is 3 larger: We input a value that is three larger for g(x) because the function takes three away before evaluating the function f.
![]()
| x | 5 | 7 | 9 | 11 |
| g(x) | 1 | 3 | 7 | 11 |
The result is that the function g(x) has been shifted to the right by 3. Notice the output values for g(x) remain the same as the output values for f(x) in the chart, but the corresponding input values, x, have shifted to the right by 3: 2 shifted to 5, 4 shifted to 7, 6 shifted to 9 and 8 shifted to 11.
Example of a Horizontal Shift with a Graph
The graph shown is a transformation of a parent function . Relate this new function g(x) to f(x), and then find a formula for g(x).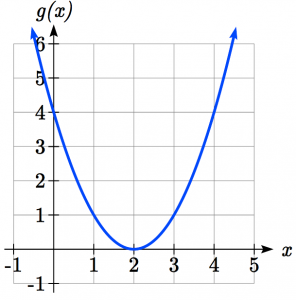
Notice that the graph looks almost identical in shape to the ![]() function, but the x values are shifted to the right two units. The vertex used to be at (0, 0) but now the vertex is at (2, 0) . The graph is the basic quadratic function shifted two to the right, so
function, but the x values are shifted to the right two units. The vertex used to be at (0, 0) but now the vertex is at (2, 0) . The graph is the basic quadratic function shifted two to the right, so ![]()
Notice how we must input the value x = 2, to get the output value y = 0; the x values must be two units larger, because of the shift to the right by 2 units.
We can then use the definition of the f(x) function to write a formula for g(x) by evaluating ![]() :
:
Since ![]() and
and ![]()
![]()
Notice how the domain and range are the same for this function. The domain is subject to change with horizontal shifts, but in this case, both are all real numbers or ![]()
If you find yourself having trouble determining whether the shift is +2 or -2, it might help to consider a single point on the graph. For a quadratic, looking at the vertex is convenient. In the original function, ![]() . In our shifted function,
. In our shifted function, ![]() . To obtain the output value of 0 from the f function, we need to decide whether a +2 or -2 will work to satisfy
. To obtain the output value of 0 from the f function, we need to decide whether a +2 or -2 will work to satisfy ![]() . For this to work, we will need to subtract 2 from our input values.
. For this to work, we will need to subtract 2 from our input values.
When thinking about horizontal and vertical shifts, it is good to keep in mind that vertical shifts are affecting the output values of the function, while horizontal shifts are affecting the input values of the function.
Example of an Application with a Shift
The function G(m) gives the number of gallons of gas required to drive m miles. Interpret ![]() and G(m+10) .
and G(m+10) .
![]() is adding 10 to the output gallons. This is 10 gallons of gas more than is required to drive m miles. So, this is the gas required to drive m miles, plus another 10 gallons of gas, or maybe the amount of gas required to drive m miles and have 10 gallons left in the tank.
is adding 10 to the output gallons. This is 10 gallons of gas more than is required to drive m miles. So, this is the gas required to drive m miles, plus another 10 gallons of gas, or maybe the amount of gas required to drive m miles and have 10 gallons left in the tank.
![]() is adding 10 to the input, miles. This is the number of gallons of gas required to drive 10 miles more than m miles. So this might be what you want if you want to give yourself a 10 mile buffer before you run out of gas.
is adding 10 to the input, miles. This is the number of gallons of gas required to drive 10 miles more than m miles. So this might be what you want if you want to give yourself a 10 mile buffer before you run out of gas.
Try it Now 2
Given the function ![]() graph the original function
graph the original function ![]() and the transformation
and the transformation ![]() .
.
a. Is this a horizontal or a vertical change?
b. Which way is the graph shifted and by how many units?
c. Graph ![]() and
and ![]() on the same axes.
on the same axes.
d. What is the domain and range of ![]() ?
?
Now that we have two transformations, we can combine them together.

Vertical Shifts are outside changes that affect the output (vertical) axis values shifting the transformed function up or down. Up if the constant is added, down if subtracted.
Horizontal Shifts are inside changes that affect the input (horizontal) axis values shifting the transformed function left or right. Right if the constant is subtracted and left if it is added.
Examples of a Functions Shifted both Horizontally and Vertically
Given ![]() , sketch a graph of
, sketch a graph of ![]() and give the new domain and range.
and give the new domain and range.
The function f is our parent absolute value function. We know that this graph has a V shape, with the point at the origin. The graph of h has transformed f in two ways: ![]() is a change on the inside of the function, giving a horizontal shift left by 1, then the subtraction by 3 in
is a change on the inside of the function, giving a horizontal shift left by 1, then the subtraction by 3 in ![]() . is a change to the outside of the function, giving a vertical shift down by 3. Transforming the graph gives:
. is a change to the outside of the function, giving a vertical shift down by 3. Transforming the graph gives:
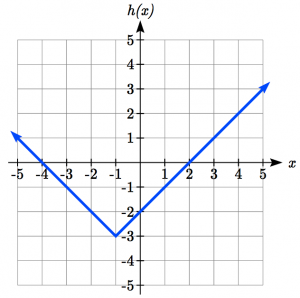
The domain of the transformed function is still ![]() , but the range has changed to
, but the range has changed to ![]() .
.
b.Write a formula for the graph shown, a transformation of the parent square root function.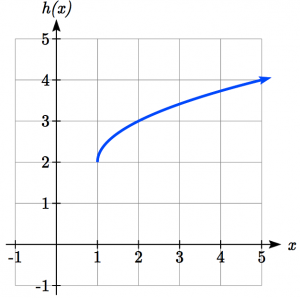
The graph of the parent function starts at the origin, so this graph has been shifted 1 to the right, and up 2. In function notation, we could write that as ![]() . Using the formula for the square root function we can write
. Using the formula for the square root function we can write ![]()
Note that this transformation has changed the domain and range of the function. This new graph has domain ![]() and range
and range ![]() .
.
Reflections
Another transformation that can be applied to a function is a reflection over the horizontal or vertical axis.
Examples
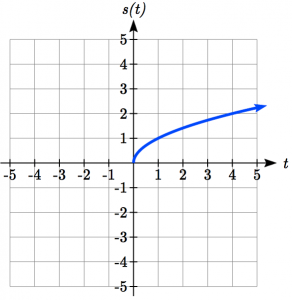
Reflect the graph of ![]() both vertically and horizontally.
both vertically and horizontally.
Reflecting the graph vertically, each output value will be reflected over the horizontal t axis:
 |
|
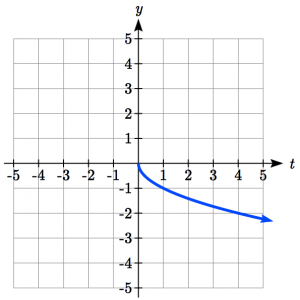 |
Since each output value is the opposite of the original output value, we can write:
![]()
![]()
Notice this is an outside change or vertical change that affects the output ![]() values so the negative sign belongs outside of the function.
values so the negative sign belongs outside of the function.
Reflecting horizontally, each input value will be reflected over the vertical axis.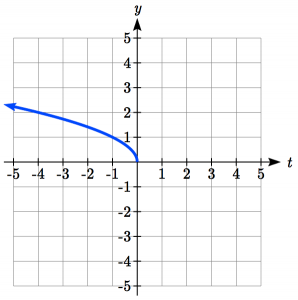
Since each input value is the opposite of the original input value, we can write:
![]()
![]()
Notice this is an inside change or horizontal change that affects the input values so the negative sign is on the inside of the function.
Note that these transformations can affect the domain and range of the functions. While the original square root function has domain ![]() and range
and range ![]() , the vertical reflection gives the
, the vertical reflection gives the ![]() function the range
function the range ![]() , and the horizontal reflection gives the
, and the horizontal reflection gives the ![]() function the domain
function the domain ![]() . (Because in order to take the square root of -t, t must be negative, for example, -2, as
. (Because in order to take the square root of -t, t must be negative, for example, -2, as ![]() .
.
Reflections
Given a function ![]() , if we define a new function
, if we define a new function ![]() as
as
![]() ,
,
then ![]() is a vertical reflection of the function
is a vertical reflection of the function ![]() , sometimes called a reflection about the x-axis or horizontal axis.
, sometimes called a reflection about the x-axis or horizontal axis.
If we define a new function ![]() as
as
![]() ,
,
then ![]() is a horizontal reflection of the function
is a horizontal reflection of the function ![]() , sometimes called a reflection about the y-axis or vertical axis.
, sometimes called a reflection about the y-axis or vertical axis.
Example of Reflections with Functions defined as Tables
A function ![]() is given as a table below. Create a table for the function
is given as a table below. Create a table for the function ![]() and
and![]()
| x | 2 | 4 | 6 | 8 |
| f(x) | 1 | 3 | 7 | 11 |
For ![]() , this is a vertical reflection, so the x values stay the same and each output value will be the opposite of the original output value:
, this is a vertical reflection, so the x values stay the same and each output value will be the opposite of the original output value:
| x | 2 | 4 | 6 | 8 |
| g(x) | -1 | -3 | -7 | -11 |
For ![]() , this is a horizontal reflection, and each input value will be the opposite of the original input value and the
, this is a horizontal reflection, and each input value will be the opposite of the original input value and the ![]() values stay the same as the
values stay the same as the ![]() values:
values:
| x | -2 | -4 | -6 | -8 |
| h(x) | 1 | 3 | 7 | 11 |
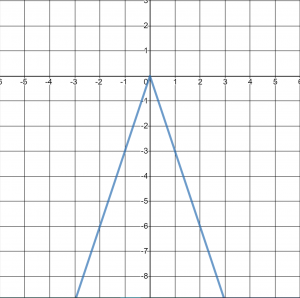
Try it Now 3
Given the parent function ![]() , graph
, graph ![]() and
and ![]() . Do you notice anything surprising?
. Do you notice anything surprising?
Stretches and Compressions
With shifts, we saw the effect of adding or subtracting to the inputs or outputs of a function. We now explore the effects of multiplying the inputs or outputs.
Remember, we can transform the inside (input values) of a function or we can transform the outside (output values) of a function. Each change has a specific effect that can be seen graphically.
Consider the function ![]() . In the parent function,
. In the parent function, ![]() , the point in the center at (0,0) is still there in
, the point in the center at (0,0) is still there in ![]() . However, what about an input of 1, the parent function has the point (1,1), but
. However, what about an input of 1, the parent function has the point (1,1), but ![]() multiplies it by 2, so the point is at (1,2). If we consider an input at 8, the parent function has a point at (8,2), but
multiplies it by 2, so the point is at (1,2). If we consider an input at 8, the parent function has a point at (8,2), but ![]() is (8,4). So the output is doubled each time. This is a vertical stretch as seen below:
is (8,4). So the output is doubled each time. This is a vertical stretch as seen below:
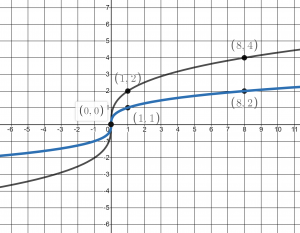
Vertical Stretch and Compression
Given a function ![]() , if we define a new function
, if we define a new function ![]() as
as
![]() , where
, where ![]() is a constant
is a constant
then ![]() is a vertical stretch or compression of the function
is a vertical stretch or compression of the function ![]() .
.
If ![]() , then the graph will be stretched
, then the graph will be stretched
If ![]() , then the graph will be compressed
, then the graph will be compressed
If ![]() , then there will be combination of a vertical stretch or compression with a vertical reflection
, then there will be combination of a vertical stretch or compression with a vertical reflection
Example of a Vertical Compression with a Table
A function ![]() is given as a table below. Create a table for the function
is given as a table below. Create a table for the function ![]()
| x | 2 | 4 | 6 | 8 |
| f(x) | 1 | 3 | 7 | 11 |
The formula ![]() tells us that the output values of
tells us that the output values of ![]() are half the output values of
are half the output values of ![]() with the same inputs. For example, we know that
with the same inputs. For example, we know that ![]() , so
, so ![]()
| x | 2 | 4 | 6 | 8 |
| g(x) | 1/2 | 3/2 | 7/2 | 11/2 |
The result is that the function ![]() has been compressed vertically by ½. Each output value has been cut in half, so the graph would now be half the original height.
has been compressed vertically by ½. Each output value has been cut in half, so the graph would now be half the original height.
Example of a Vertical Stretch/Compression of a Graph
The graph shown is a transformation of the parent function ![]() .
. 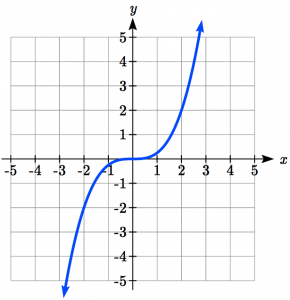 Relate this new function
Relate this new function ![]() to
to ![]() , then find a formula for
, then find a formula for ![]() .
.
When trying to determine a vertical stretch or shift, it is helpful to look for a point on the graph that is relatively clear. In this graph, it appears that ![]() With the basic cubic function at the same input,
With the basic cubic function at the same input, ![]()
Based on that, it appears that the outputs of g are ¼ the outputs of the function f, since
![]()
From this we can fairly safely conclude that:
![]()
We can write a formula for ![]() by using the definition of the function
by using the definition of the function ![]()
![]()
Try it Now 4
Use the parent function ![]() to graph
to graph ![]() and give the domain and range of
and give the domain and range of ![]() .
.
Horizontal stretches and compressions are also possible, but we can usually re-write the function so that this is a vertical stretch or compression. For example, a horizontal compression of the function ![]() by ½ would result in a new function
by ½ would result in a new function ![]() , but this can also be written as
, but this can also be written as ![]() , a vertical stretch of
, a vertical stretch of ![]() by 4. When writing a formula for a transformed parent function, we only need to find one transformation that would produce the graph.
by 4. When writing a formula for a transformed parent function, we only need to find one transformation that would produce the graph.
Combining Transformations
When combining transformations, it is very important to consider the order of the transformations. For example, vertically shifting by 3 and then vertically stretching by 2 does not create the same graph as vertically stretching by 2 then vertically shifting by 3.
When we see an expression like ![]() , which transformation should we start with? The answer here follows nicely from order of operations, for outside transformations. Given the output value of
, which transformation should we start with? The answer here follows nicely from order of operations, for outside transformations. Given the output value of ![]() , we first multiply by 2, causing the vertical stretch, then add 3, causing the vertical shift. (Multiplication before Addition)
, we first multiply by 2, causing the vertical stretch, then add 3, causing the vertical shift. (Multiplication before Addition)
Combining Vertical Transformations
When combining vertical transformations written in the form ![]() ,
,
first vertically stretch by a, then vertically shift by k.
Horizontal transformations are a little trickier to think about. When we write ![]() for example, we have to think about how the inputs to the g function relate to the inputs to the f function. Suppose we know
for example, we have to think about how the inputs to the g function relate to the inputs to the f function. Suppose we know ![]() . What input to g would produce that output? In other words, what value of x will allow
. What input to g would produce that output? In other words, what value of x will allow ![]() ? We would need 3-x=12. To solve for x, we would first subtract 3, resulting in horizontal shift, then multiply by -1, causing a horizontal reflection.
? We would need 3-x=12. To solve for x, we would first subtract 3, resulting in horizontal shift, then multiply by -1, causing a horizontal reflection.
Independence of Horizontal and Vertical Transformations
Horizontal and vertical transformations are independent. It does not matter whether horizontal or vertical transformations are done first.
Example of Several Transformations with a Table
Given the table of values for the function ![]() below, create a table of values for the function
below, create a table of values for the function ![]()
| x | 6 | 12 | 18 | 24 |
| f(x) | 10 | 14 | 15 | 17 |
There are 3 steps to this transformation and we will work from the inside out. Starting with the horizontal transformations, is a horizontal shift to the left by 2, which means we subtract each x value by 2.
| x | 4 | 10 | 16 | 22 |
| f(x+2) | 10 | 14 | 15 | 17 |
Looking now to the vertical transformations, we start with the vertical stretch, which will multiply the output values by 3. We apply this to the previous transformation.
| x | 4 | 10 | 16 | 22 |
| 3f(x+2) | 30 | 42 | 45 | 51 |
Finally, we can apply the vertical shift, which will add 1 to all the output values.
| x | 4 | 10 | 16 | 22 |
| 3f(x+2)+1 | 31 | 43 | 46 | 52 |
Example of Multiple Transformation of a Graph
Use the parent function ![]() , sketch a graph of
, sketch a graph of ![]()
First, we see that 2 in the denominator and we did not cover horiztonal stretches, so we will change this slightly to ![]() . This makes a little easier to see that the -1/2 is just a vertical compression and reflection.
. This makes a little easier to see that the -1/2 is just a vertical compression and reflection.
See the animation below: We begin with our parent function: ![]() .
.
Let’s start with our horizontal (inside) transformation and graph ![]() which is just a shift of 3 to the left.
which is just a shift of 3 to the left.
Then, we will do our vertical transformations, starting with a vertical compression by 1/2 and then a reflection across the x-axis.
Finally we have the vertical shift of 1 unit down.
Example Writing a Transformed Function from the Graph
Write an equation for the transformed graph function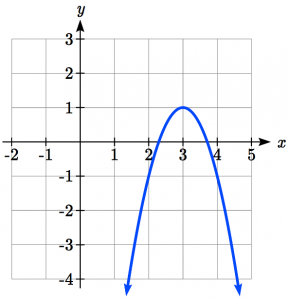 shown and give the domain and range.
shown and give the domain and range.
This looks like a parabola so let’s try our parent function ![]()
Observing the graph, we notice several transformations:
The original parent function has been flipped over the x axis, a vertical stretch has occurred, and we can see a shift to the right 3 units and a shift up 1 unit.
In total there are four operations:
- Vertical reflection, requiring a negative sign outside the function
- Vertical Stretch of 2 (remember that concave down parabolas start with over 1 down 1, this one is over 1, down 2)
- Horizontal Shift Right 3 units, which tells us to put
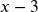 on the inside of the function
on the inside of the function - Vertical Shift up 1 unit, telling us to add 1 on the outside of the function
So this takes our parent function, ![]() :
:
- First do the horizontal shift
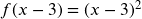
- Now the Stretch:
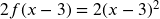
- Now the Reflection:
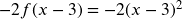
- And now the vertical shift:
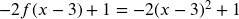
This looks familiar, it is the vertex form of a parabola! If you had trouble figuring out the transformations, that’s okay. We can still find the formula for a parabola using the techniques we discussed in chapter 5. All we need is the vertex and another point.
The domain is still ![]() but the range is now
but the range is now ![]()
Try it Now 5
a. Try graphing ![]() and give the domain and range.
and give the domain and range.
b. Try to figure out the what the parent function (it’s one of the ones at the beginning of the section) and transformations are, figure out the domain and range and write an equation for this graph:
Try it Now Answers
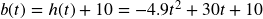
- a. Horizontal shift
b. The function is shifted to the LEFT by 2 units
c.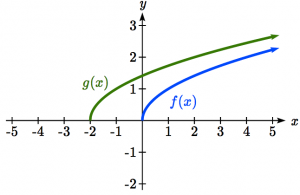
Answer Graph 2c d. Domain:
 Range:
Range: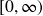
- Notice
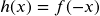 looks the same as
looks the same as 
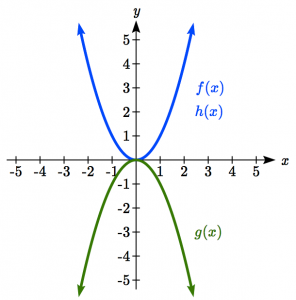
Answer Graph 3 - Domain:
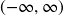 Range:
Range: ![Rendered by QuickLaTeX.com (-\infty,0]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9c3f5062653097ec21c4a3247c963848_l3.png)
Answer Graph 4 - a. Domain:
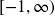 Range:
Range: 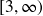
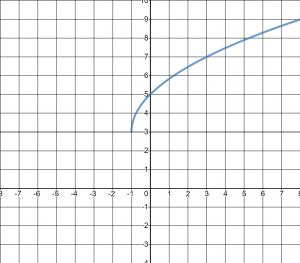
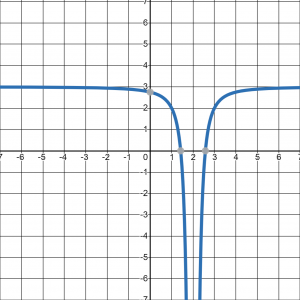
Answer Graph 5a b. The parent function is the square reciprocal:
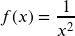 . It is shifted right 2 units, reflected on the x-axis and up 3:
. It is shifted right 2 units, reflected on the x-axis and up 3: 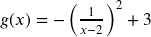
Domain:
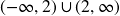 Range:
Range: 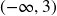
Media Attributions
- linear
- absvalue
- square
- cubic
- sqroot
- cuberoot
- recip
- squaredrecip
- graphofverticalshift
- graphofhorizshift
- 66example6
- Reminder is licensed under a Public Domain license
- 67example1
- 67example2
- 67example3
- 67example4
- 67example5
- graphofvertstretch
- 67example7
- 67example6
- TIN67
- tinasnwer672
- tinanswer673
- tinanswer674
- tinanswer675

