3.4 Solving Systems with Inverses
Nancy plans to invest $10,500 into two different bonds to spread out her risk. The first bond has an annual return of 10%, and the second bond has an annual return of 6%. In order to receive an 8.5% return from the two bonds, how much should Nancy invest in each bond? What is the best method to solve this problem?
There are several ways we can solve this problem. As we have seen in previous sections, systems of equations and matrices are useful in solving real-world problems involving finance. After studying this section, we will have the tools to solve the bond problem using the inverse of a matrix.
Finding the Inverse of a Matrix
The multiplicative inverse of a real number ![]() is
is ![]() , where the product is 1:
, where the product is 1: ![]() . For example,
. For example, ![]() . and The multiplicative inverse of a matrix is similar in concept, except that the product of matrix
. and The multiplicative inverse of a matrix is similar in concept, except that the product of matrix ![]() and its inverse
and its inverse ![]() equals the identity matrix. The identity matrix is a square matrix containing ones down the main diagonal and zeros everywhere else. We identify identity matrices by
equals the identity matrix. The identity matrix is a square matrix containing ones down the main diagonal and zeros everywhere else. We identify identity matrices by ![]() where
where ![]() represents the dimension of the matrix. Shown below are the identity matrices for a
represents the dimension of the matrix. Shown below are the identity matrices for a ![]() matrix and a
matrix and a ![]() matrix, respectively.
matrix, respectively.
![Rendered by QuickLaTeX.com \[{I_2} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right]\,\,\,\,\,\,\,\qquad{I_3} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-58df9226daea802dfb4080a43c76506c_l3.png)
The identity matrix acts as a 1 in matrix algebra. For example, ![]() . A matrix that has a multiplicative inverse has the properties:
. A matrix that has a multiplicative inverse has the properties:
![]()
A matrix that has a multiplicative inverse is called an invertible matrix. Only a square matrix may have a multiplicative inverse, as the reversibility, ![]() , is a requirement. Not all square matrices have an inverse, but if
, is a requirement. Not all square matrices have an inverse, but if ![]() is invertible, then
is invertible, then ![]() is unique. We will look at two methods for finding the inverse of a
is unique. We will look at two methods for finding the inverse of a ![]() matrix and a technology approach that can be used on any size matrix.
matrix and a technology approach that can be used on any size matrix.
The Identity Matrix and the Multiplicative Inverse
The identity matrix, ![]() , is a square matrix containing ones down the main diagonal and zeros everywhere else.
, is a square matrix containing ones down the main diagonal and zeros everywhere else.
![Rendered by QuickLaTeX.com \[\begin{array}{l} {I_2} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right]\,\,\,\,\,\,\,\,\,{I_3} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right]\\ \,\,\,\quad \quad 2 \times 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad \quad 3 \times 3 \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8f3097dc4e47e86067ec5cdafe5e0561_l3.png)
If ![]() is an
is an ![]() matrix and
matrix and ![]() is an
is an ![]() matrix such that
matrix such that ![]() then
then ![]() is the multiplicative inverse of a matrix
is the multiplicative inverse of a matrix ![]() .
.
Example of the Multiplicative Inverse in Action
Given matrix A, show that ![]()
![]()
Use matrix multiplication to show that the product of ![]() and the identity is equal to the product of the identity and
and the identity is equal to the product of the identity and ![]() .
.
![]()
![]()
Showing that one Matrix is the multiplicative inverse of the another
- Given matrix
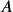 of order
of order 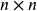 and matrix
and matrix 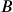 of order
of order 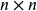 , multiply
, multiply 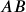 .
. - If
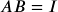 , then find the product
, then find the product 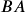 . If
. If 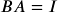 , then
, then 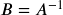 and
and 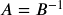 .
.
Example showing two matrices are multiplicative inverses
Show that the given matrices are multiplicative inverses of each other.
![]()
Multiply ![]() and
and ![]() . If both products equal the identity, then the two matrices are inverses of each other.
. If both products equal the identity, then the two matrices are inverses of each other.
![Rendered by QuickLaTeX.com \begin{array}{c} AB = \left[ {\begin{array}{*{20}{c}} 1&5\\ { - 2}&{ - 9} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} { - 9}&{ - 5}\\ 2&1 \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} {1\left( { - 9} \right) + 5\left( 2 \right)}&{1\left( { - 5} \right) + 5\left( 1 \right)}\\ { - 2\left( { - 9} \right) - 9\left( 2 \right)}&{ - 2\left( { - 5} \right) - 9\left( 1 \right)} \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right] \end{array}](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-784e432249e4b4e496d494ff7f899039_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c} BA = \left[ {\begin{array}{*{20}{c}} { - 9}&{ - 5}\\ 2&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} 1&5\\ { - 2}&{ - 9} \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} { - 9\left( 1 \right) - 5\left( { - 2} \right)}&{ - 9\left( 5 \right) - 5\left( { - 9} \right)}\\ {2\left( 1 \right) + 1\left( { - 2} \right)}&{2\left( { - 5} \right) + 1\left( { - 9} \right)} \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right] \end{array}](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2ee4e9e4efbdf453b297903a58b6fdfe_l3.png)
![]() and
and ![]() are inverses of each other.
are inverses of each other.
Try it Now 1
Show that the following two matrices are inverses of each other.
![]()
Finding the Multiplicative Inverse by Augmenting with the Identity
One way to find the multiplicative inverse is by augmenting with the identity. When matrix ![]() is transformed into
is transformed into ![]() , the augmented matrix,
, the augmented matrix, ![]() transforms into
transforms into ![]() .
.
For example, given
![]()
Augment ![]() with the identity
with the identity
![Rendered by QuickLaTeX.com \left[ {\begin{array}{*{20}{c}} 2&1\\ 5&3 \end{array}\,\,\,\left| {\,\,\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right.} \right]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5e72bbd6f9d23bb63e15a59a089fc96e_l3.png)
Perform row operations with the goal of turning ![]() into the identity.
into the identity.
- Divide row 1 by 2.
![Rendered by QuickLaTeX.com \[\left[ {\begin{array}{*{20}{c}} 1&\frac{1}{2}\\ 5&3 \end{array}\,\,\,\left| {\,\,\,\begin{array}{*{20}{c}} \frac{1}{2}&0\\ 0&1 \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ae5a69c6f66db705cb9212aa99e98815_l3.png)
- Multiply row 1 by –5 and add to row 2.
![Rendered by QuickLaTeX.com \[\left[ {\begin{array}{*{20}{c}} 1&\frac{1}{2}\\ 0&\frac{1}{2} \end{array}\,\,\,\left| {\,\,\,\begin{array}{*{20}{c}} \frac{1 }{2}&0\\ \frac{-5}{2}&1 \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-06d6c2e0c3541ea09ef8bfd17b775b51_l3.png)
- Multiply row 2 by 2.
![Rendered by QuickLaTeX.com \[\left[ {\begin{array}{*{20}{c}} 1&\frac{1}{2}\\ 0&1 \end{array}\,\,\,\left| {\,\,\begin{array}{*{20}{c}} \frac{1 }{2}&0\\ -5&{ 2} \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-dc8ffd4181e0d0322ee885d7a5e6ae9a_l3.png)
- Multiply row 2 by
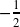 and add to row 1
and add to row 1
![Rendered by QuickLaTeX.com \[\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}\,\,\,\left| {\,\,\,\begin{array}{*{20}{c}} 3&{- 1}\\ -5&{2} \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-916bf55756b8f60a79865c6b9dd8355f_l3.png)
The matrix we have found is ![]() .
.
![]()
Finding the Multiplicative Inverse of 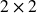 Matrices Using a Formula
Matrices Using a Formula
When we need to find the multiplicative inverse of a matrix, we can use a special formula instead of using matrix multiplication or augmenting with the identity.
Formula for the Inverse of a 2 by 2 Matrix
If ![]() is a
is a ![]() matrix, such as
matrix, such as ![]()
the multiplicative inverse of a ![]() is given by the formula
is given by the formula
![]()
where ![]() . If
. If ![]() then
then ![]() has no inverse.
has no inverse.
A good way to remember this is that we switch the diagonals of the matrix and make the off-diagonals opposite.
Example Finding the Inverse of a ![]() Matrix with the Formula
Matrix with the Formula
Use the formula to find the multiplicative inverse of
![]()
Using the formula, we have
![Rendered by QuickLaTeX.com \begin{array}{c} {A^{ - 1}} = \frac{1}{{\left( 2 \right)\left( 3 \right) - \left( 5 \right)\left( 1 \right)}}\left[ {\begin{array}{*{20}{c}} 3&{ - 1}\\ { - 5}&2 \end{array}} \right]\\ = \frac{1}{1}\left[ {\begin{array}{*{20}{c}} 3&{ - 1}\\ { - 5}&2 \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} 3&{ - 1}\\ { - 5}&2 \end{array}} \right] \end{array}](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-02b22351024df3981994726b6156045a_l3.png)
Notice this matches the inverse we found above by augmenting with the identity matrix but was a lot quicker and easier.
Try it Now 2
Use the formula to find the inverse of matrix ![]()
Example of a non-invertible matrix
Find the inverse, if it exists, of the given matrix: ![]()
We will use the method of augmenting with the identity.
![Rendered by QuickLaTeX.com \left[ {\begin{array}{*{20}{c}} 3&6\\ 1&3 \end{array}\,\,\,\left| {\,\,\,\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right.} \right]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-28b4539e069b7b8e6dbd226d968dd778_l3.png)
Switch row 1 and row 2.
![Rendered by QuickLaTeX.com \left[ {\begin{array}{*{20}{c}} 1&3\\ 3&{6\,} \end{array}\,\,\left| {\,\,\,\begin{array}{*{20}{c}} 0&1\\ 1&0 \end{array}} \right.} \right]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e852e4df8e2e4cacce1521233fc451df_l3.png)
Multiply row 1 by and add it to row 2.
![Rendered by QuickLaTeX.com \left[ {\begin{array}{*{20}{c}} 1&2\\ 0&0 \end{array}\,\,\,\left| {\,\,\,\begin{array}{*{20}{c}} 1&0\\ { - 3}&1 \end{array}} \right.} \right]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-95a796d5b298fb55cf4d728bb94a8ea2_l3.png)
Now that we have a row of zeroes on the left, there is nothing further we can do. The zeros in row 2 indicate that this matrix has no inverse.
We could have also used the ![]() formula to see this as well. In this case, it would be
formula to see this as well. In this case, it would be ![]() so it is not invertible.
so it is not invertible.
Finding the Multiplicative Inverse of Matrices
Unfortunately, we do not have a formula similar to the one for a ![]() matrix to find the inverse of a
matrix to find the inverse of a ![]() matrix. Instead, we will augment the original matrix with the identity matrix and use row operations to obtain the inverse.
matrix. Instead, we will augment the original matrix with the identity matrix and use row operations to obtain the inverse.
Given a ![]() matrix:
matrix:
![Rendered by QuickLaTeX.com \[A = \left[ {\begin{array}{*{20}{c}} 2&3&1\\ 3&3&1\\ 2&4&1 \end{array}} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-524be5aad195eeb99a4a19aa6fe5a7e1_l3.png)
Augment ![]() with the identity matrix
with the identity matrix
![Rendered by QuickLaTeX.com \[A\left| I \right. = \left[ {\begin{array}{*{20}{c}} 2&3&1\\ 3&3&1\\ 2&4&1 \end{array}\,\,\left| {\,\,\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9afe0f7c262524d0683b7ba9dc240bdb_l3.png)
To begin, we write the augmented matrix with the identity on the right and on the left. Performing elementary row operations so that the identity matrix appears on the left, we will obtain the inverse matrix on the right. We will find the inverse of this matrix in the next example.
Finding the Inverse of a ![]() Matrix
Matrix
- Write the original matrix augmented with the identity matrix on the right.
- Use elementary row operations so that the identity appears on the left.
- What is obtained on the right is the inverse of the original matrix.
- Use matrix multiplication to show that
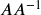 and
and 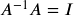 .
.
Example Finding the Inverse of a ![]() Matrix
Matrix
Given the ![]() matrix
matrix ![]() , find the inverse.
, find the inverse.
![Rendered by QuickLaTeX.com A = \left[ {\begin{array}{*{20}{c}} 2&3&1\\ 3&3&1\\ 2&4&1 \end{array}} \right]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9279a7384300d5e41533627523b3eb45_l3.png)
Augment ![]() with the identity matrix, and then begin row operations until the identity matrix replaces
with the identity matrix, and then begin row operations until the identity matrix replaces ![]() . The matrix on the right will be the inverse of
. The matrix on the right will be the inverse of ![]() .
.
![Rendered by QuickLaTeX.com \[Switch R_1 and R_2 \rightarrow \left[ {\begin{array}{*{20}{c}} 2&3&1\\ 3&3&1\\ 2&4&1 \end{array}\,\,\,\left| {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ {\,\,0}&0&1 \end{array}} \right.} \right] \longrightarrow \left[ {\begin{array}{*{20}{c}} 3&3&1\\ 2&3&1\\ 2&4&1 \end{array}\,\,\,\left| {\begin{array}{*{20}{c}} 0&1&0\\ 1&0&0\\ {\,\,\,0}&0&1 \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-78a78f7882dc49029c661a8ad9bb4bcd_l3.png)
![Rendered by QuickLaTeX.com \[ - {R_2} + {R_1} = {R_1} \to \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 2&3&1\\ 2&4&1 \end{array}\,\,\,\left| {\,\,\begin{array}{*{20}{c}} { - 1}&1&0\\ 1&0&0\\ 0&0&1 \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fb2b20585ed4c3b872711ca6a88b024f_l3.png)
![Rendered by QuickLaTeX.com \[ - {R_2} + {R_3} = {R_3} \to \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 2&3&1\\ 0&1&0 \end{array}\left| {\,\,\begin{array}{*{20}{c}} { - 1}&1&0\\ {\,\,1}&0&0\\ { - 1}&0&1 \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-035ad1ff1a29548f266a78d8847b318d_l3.png)
![Rendered by QuickLaTeX.com \[{R_3}\, \leftrightarrow {\rm{ }}{R_2} \to \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 2&3&1 \end{array}\,\,\left| {\,\,\begin{array}{*{20}{c}} { - 1}&1&0\\ { - 1}&0&1\\ {\,\,\,1}&0&0 \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f998f44efa3f94c3d04205802bbfaa76_l3.png)
![Rendered by QuickLaTeX.com \[ - 2{R_1} + {R_3} = {R_3} \to \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&3&1 \end{array}\,\,\left| {\,\begin{array}{*{20}{c}} { - 1}&1&0\\ { - 1}&0&1\\ 3&{ - 2}&0 \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-0aa66d34a45cc5652eca38ee7de3fc21_l3.png)
![Rendered by QuickLaTeX.com \[ - 3{R_2} + {R_3} = {R_3} \to \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&{\,1\,\,} \end{array}\left| {\,\,\begin{array}{*{20}{c}} { - 1}&{\,\,1}&{\,\,0}\\ { - 1}&{\,\,0}&{\,\,\,1}\\ {\,\,6}&{ - 2}&{ - 3} \end{array}} \right.} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b53dd06545cc9423cc4964db8bcf0d50_l3.png)
Thus,
![Rendered by QuickLaTeX.com {A^{ - 1}} = B = \left[ {\begin{array}{*{20}{c}} { - 1}&{\,1}&{\,0}\\ { - 1}&{\,\,0}&{\,\,1}\\ {\,\,6}&{ - 2}&{ - 3} \end{array}\,} \right]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5c34ba813b59d92f4e1e6c36e2d3e260_l3.png)
To prove that ![]() , let’s multiply the two matrices together to see if the product equals the identity, if
, let’s multiply the two matrices together to see if the product equals the identity, if ![]() and
and ![]()
![Rendered by QuickLaTeX.com \[\begin{array}{c} A{A^{ - 1}} = \left[ {\begin{array}{*{20}{c}} 2&3&1\\ 3&3&1\\ 2&4&1 \end{array}} \right]\left[ {\,\begin{array}{*{20}{c}} { - 1}&{\,1}&0\\ { - 1}&{\,\,0}&{\,1}\\ 6&{ - 2}&{ - 3} \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} {2\left( { - 1} \right) + 3\left( { - 1} \right) + 1\left( 6 \right)}&{2\left( 1 \right) + 3\left( 0 \right) + 1\left( { - 2} \right)}&{2\left( 0 \right) + 3\left( 1 \right) + 1\left( { - 3} \right)}\\ {3\left( { - 1} \right) + 3\left( { - 1} \right) + 1\left( 6 \right)}&{3\left( 1 \right) + 3\left( 0 \right) + 1\left( { - 2} \right)}&{3\left( 0 \right) + 3\left( 1 \right) + 1\left( { - 3} \right)}\\ {2\left( { - 1} \right) + 4\left( { - 1} \right) + 1\left( 6 \right)}&{2\left( 1 \right) + 4\left( 0 \right) + 1\left( { - 2} \right)}&{2\left( 0 \right) + 4\left( 1 \right) + 1\left( { - 3} \right)} \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right] \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-9046a1f97176038b4ad2508460cd4e83_l3.png)
![Rendered by QuickLaTeX.com \[\begin{array}{c} {A^{ - 1}}A = \left[ {\,\begin{array}{*{20}{c}} { - 1}&{\,1}&0\\ { - 1}&{\,\,0}&{\,1}\\ 6&{ - 2}&{ - 3} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 2&3&1\\ 3&3&1\\ 2&4&1 \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} { - 1(2) + 1(3) + 0(2)}&{ - 1(3) + 1(3) + 0(4)}&{ - 1(1) + 1(1) + 0(1)}\\ { - 1(2) + 0(3) + 1(2)}&{ - 1(3) + 0(3) + 1(4)}&{ - 1(1) + 0(1) + 1(1)}\\ {6(2) + - 2(3) + - 3(2)}&{6(3) + - 2(3) + - 3(4)}&{6(1) + - 2(1) + - 3(1)} \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right] \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-725e2bc2977bb61ec34e7874c93093d5_l3.png)
This is of course, a difficult and tedious process. On a TI calculator, once your matrix is in the calculator, you can simply call up matrix [A] by 2nd ![]() enter. Then you can use the
enter. Then you can use the ![]() enter key to invert it. Casio has similar functions and Excel has a =MINVERSE command to do this as well.
enter key to invert it. Casio has similar functions and Excel has a =MINVERSE command to do this as well.
Try it Now 3
Find the inverse of the ![]() matrix.
matrix.
![Rendered by QuickLaTeX.com A = \left[ {\begin{array}{*{20}{c}} {\,\,2}&{ - 17}&{11}\\ { - 1}&{\,\,\,11}&{ - 7}\\ {\,\,\,0}&{\,\,\,\,\,3}&{ - 2} \end{array}} \right]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f2071f4154b7435a30712752e4cf23eb_l3.png)
Solving a System of Linear Equations Using the Inverse of a Matrix
Solving a system of linear equations using the inverse of a matrix requires the definition of two new matrices: ![]() is the matrix representing the variables of the system, and
is the matrix representing the variables of the system, and ![]() is the matrix representing the constants. Using matrix multiplication, we may define a system of equations with the same number of equations as variables as:
is the matrix representing the constants. Using matrix multiplication, we may define a system of equations with the same number of equations as variables as:
![]() .
.
To solve a system of linear equations using an inverse matrix, let ![]() be the coefficient matrix, let
be the coefficient matrix, let ![]() be the variable matrix, and let
be the variable matrix, and let ![]() be the constant matrix. Thus, we want to solve a system
be the constant matrix. Thus, we want to solve a system ![]() . For example, look at the following system of equations.
. For example, look at the following system of equations.
![]()
From this system, the coefficient matrix is
![]()
The variable matrix is
![]()
And the constant matrix is
![]()
Then looks like
![]()
Solving this system of equations written in matrix form is similar to solving a linear equation, except there is no matrix “division” so instead we need to use the inverse. The goal is the same—to isolate the variable. We will investigate this idea in detail, but it is helpful to begin with a ![]() system and then move on to a
system and then move on to a ![]() system.
system.
First consider the matrix equation: ![]()
Multiply both sides by the inverse of ![]() to obtain the solution.
to obtain the solution.
![Rendered by QuickLaTeX.com \[\begin{array}{c} \left( {{A^{ - 1}}} \right)AX = \left( {{A^{ - 1}}} \right)B\\ \left[ {\left( {{A^{ - 1}}} \right)A} \right]X = \left( {{A^{ - 1}}} \right)B\\ IX = \left( {{A^{ - 1}}} \right)B\\ X = \left( {{A^{ - 1}}} \right)B \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-00ad29f6b16735c70661f5f048b480b2_l3.png)
Solving a System of Equations Using the Inverse of a Matrix
Given a system of equations, write the coefficient matrix ![]() the variable matrix
the variable matrix ![]() and the constant matrix
and the constant matrix ![]() . Then
. Then
![]()
If matrix ![]() is invertible, then the solution to this system is:
is invertible, then the solution to this system is:
![]()
 If the coefficient matrix does not have an inverse, the system could be inconsistent and have no solution, or be dependent and have infinitely many solutions. At this point, we need to use the row-reduction method to determine which it is and if dependent, give the general solution.
If the coefficient matrix does not have an inverse, the system could be inconsistent and have no solution, or be dependent and have infinitely many solutions. At this point, we need to use the row-reduction method to determine which it is and if dependent, give the general solution.
Example Solving a ![]() System using Inverse
System using Inverse
Solve the given system of equations using the inverse of a matrix.
![]()
Write the system in terms of a coefficient matrix, a variable matrix, and a constant matrix.
![]()
Then
![]()
Using the formula to calculate ![]() , we have:
, we have:
![Rendered by QuickLaTeX.com \begin{array}{l} {A^{ - 1}} = \frac{1}{{ad - bc}}\left[ {\begin{array}{*{20}{c}} d&{ - b}\\ { - c}&a \end{array}} \right]\\ \;\;\;\;\; = \frac{1}{{3(11) - 8(4)}}\left[ {\begin{array}{*{20}{c}} {11}&{ - 8}\\ { - 4}&3 \end{array}} \right]\\ \;\;\;\;\; = \frac{1}{1}\left[ {\begin{array}{*{20}{c}} {11}&{ - 8}\\ { - 4}&3 \end{array}} \right] \end{array}](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-b1c21b1175fc227e29eeb0c9741dc9f8_l3.png)
![]()
Now we are ready to solve. Multiply both sides of the equation by ![]() .
.
![Rendered by QuickLaTeX.com \begin{array}{c} X = \left( {{A^{ - 1}}} \right)B\\ \left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {11}&{ - 8}\\ { - 4}&3 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 5\\ 7 \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] = \left[ \begin{array}{c} 11\left( 5 \right) + \left( { - 8} \right)7\\ - 4\left( 5 \right) + 3\left( 7 \right) \end{array} \right]\\ \left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 1}\\ {\,\,1} \end{array}} \right] \end{array}](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-49676781bec3ded8b6ca40fc13c22f3a_l3.png)
The solution is (-1,1).
 Note that you cannot solve for
Note that you cannot solve for ![]() by finding the product
by finding the product ![]() . Recall the matrix multiplication is not commutative, so
. Recall the matrix multiplication is not commutative, so ![]() . Consider our steps for solving the matrix equation.
. Consider our steps for solving the matrix equation.
![Rendered by QuickLaTeX.com \[\begin{array}{c} \left( {{A^{ - 1}}} \right)AX = \left( {{A^{ - 1}}} \right)B\\ \left[ {\left( {{A^{ - 1}}} \right)A} \right]X = \left( {{A^{ - 1}}} \right)B\\ IX = \left( {{A^{ - 1}}} \right)B\\ X = \left( {{A^{ - 1}}} \right)B \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-00ad29f6b16735c70661f5f048b480b2_l3.png)
Notice in the first step we multiplied both sides of the equation by ![]() , but the
, but the ![]() was to the left of on both sides of the equation. Matrix multiplication is not commutative, order matters.
was to the left of on both sides of the equation. Matrix multiplication is not commutative, order matters.
Systems of equations in many variables can get very complex, but solving using matrices can easily be handled by calculators or computers.
Solve Systems of Equations using Matrix Inversion in a Calculator
- Save the coefficient matrix and the constant matrix as matrix variables
![Rendered by QuickLaTeX.com [A]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4718835b27c9309a312ec36d718f0921_l3.png) and
and ![Rendered by QuickLaTeX.com [B]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-d11d249b469c1971d67f76eec27767c5_l3.png) .
. - Enter the multiplication into the calculator, calling up each matrix variable as needed.
![Rendered by QuickLaTeX.com [A]\rightarrow x^{-1} \rightarrow [B]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-bad75d55d9c760a9180cbfe147caccc4_l3.png)
- If the coefficient matrix,
![Rendered by QuickLaTeX.com [A]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4718835b27c9309a312ec36d718f0921_l3.png) is invertible, the calculator will present the solution matrix; if
is invertible, the calculator will present the solution matrix; if ![Rendered by QuickLaTeX.com [A]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-4718835b27c9309a312ec36d718f0921_l3.png) is not invertible, the calculator will present an error message.
is not invertible, the calculator will present an error message.
See these videos for this on a TI-83/84 and CASIO.
This can also be accomplished in Excel using =MINVERSE and =MMULT.
Example Solving a System Using Inverses and Technology
Solve the following system using the inverse of a matrix.
![Rendered by QuickLaTeX.com \[\begin{array}{c} 5x + 15y + 56z = 35\\ - 4x - 11y - 41z = - 26\\ - x - 3y - 11z = - 7 \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-ca9f021767b87ceb21e47fdfcf149041_l3.png)
Write the equation ![]()
![Rendered by QuickLaTeX.com \[\left[ {\begin{array}{*{20}{c}} 5&{15}&{56}\\ { - 4}&{ - 11}&{ - 41}\\ { - 1}&{ - 3}&{ - 11} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x\\ y\\ z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {35}\\ { - 26}\\ { - 7} \end{array}} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-606544af3859acd48907b6c5761f558f_l3.png)
Step 1: Enter the coefficient matrix into [A]:
- 2nd
- 3 rows and 3 columns and enter in all the values hitting Enter in between each.
- 2nd Mode to leave the screen.
Step 2: Enter the constant matrix into [B]:
- 2nd
- 3 rows and 1 columns and enter in all the values hitting Enter in between each.
- 2nd Mode to leave the screen.
Step 3: Type in the equation for X
- 2nd
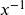 Enter to bring up [A]
Enter to bring up [A] 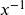 to make A inverse
to make A inverse- 2nd
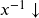 to bring up [B] Enter.
to bring up [B] Enter.
The calculator now displays:
![]()
So we know the solution is (1,2,0).
Try it Now 4
Solve the system using the inverse of the coefficient matrix.
![Rendered by QuickLaTeX.com \[\begin{array}{c} 2x - 17y + 11z = 0\\ - x + 11y - 7z = 8\\ 3y - 2z = - 2 \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-fcd96679668d8ce27efba7dd79f0971a_l3.png)
Try it Now Answers
So ![]()
Media Attributions
- warningsign
- takenote is licensed under a Public Domain license

![Rendered by QuickLaTeX.com \[\begin{array}{l} AB = \left[ {\begin{array}{*{20}{c}} {\,\,1}&{\,4}\\ { - 1}&{ - 3} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} { - 3}&{ - 4}\\ {\,\,\,1}&{\,\,\,1} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1\left( { - 3} \right) + 4\left( 1 \right)}&{1\left( { - 4} \right) + 4\left( 1 \right)}\\ { - 1\left( { - 3} \right) + - 3\left( 1 \right)}&{ - 1\left( { - 4} \right) + - 3\left( 1 \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right]\\ BA = \left[ {\begin{array}{*{20}{c}} { - 3}&{ - 4}\\ {\,\,\,1}&{\,\,\,1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\,\,1}&{\,4}\\ { - 1}&{ - 3} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - 3(1) + - 4( - 1)}&{ - 3(4) + - 4( - 3)}\\ {1(1) + 1( - 1)}&{1(4) + 1( - 3)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right] \end{array}\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-911a182070ca083fc83697581d345778_l3.png)
![Rendered by QuickLaTeX.com {A^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {\frac{3}{5}}&{\frac{1}{5}}\\ { - \frac{2}{5}}&{\frac{1}{5}} \end{array}} \right]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-e740a9ed3ab9a3ce21eedb8f5cd13d1e_l3.png)
![Rendered by QuickLaTeX.com {A^{ - 1}} = \left[ {\begin{array}{*{20}{c}} 1&1&{\,\,2}\\ 2&4&{ - 3}\\ 3&6&{ - 5} \end{array}} \right]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-5e8ff3e7c24c2dd2e6a82857839dee84_l3.png)
![Rendered by QuickLaTeX.com \[X = \left[ {\begin{array}{*{20}{c}} 4\\ {38}\\ {58} \end{array}} \right]\]](https://ua.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-a3a2aa8e7e376e4c850482dfad70d93f_l3.png)
